알고리즘 : 상호 배타 집합 알고리즘 (Java)

상호 배타 집합 알고리즘

 

• Disjoint Set 알고리즘, 분리집합 알고리즘, Union-Find 알고리즘 이라고도 불림
• 그래프, 트리에서 많이 사용
• 동일한 집합에 속하는지 여부를 판단하고, 서로 다른 집합을 합치는 연산에 관한 알고리즘

 

 

 

 

상호 배타 집합의 주요 연산

 

 

 

1. Make-Set

새로운 집합을 생성하는 연산. 자기 자신을 부모로 설정하여 트리 형태로 관리

 

 

 

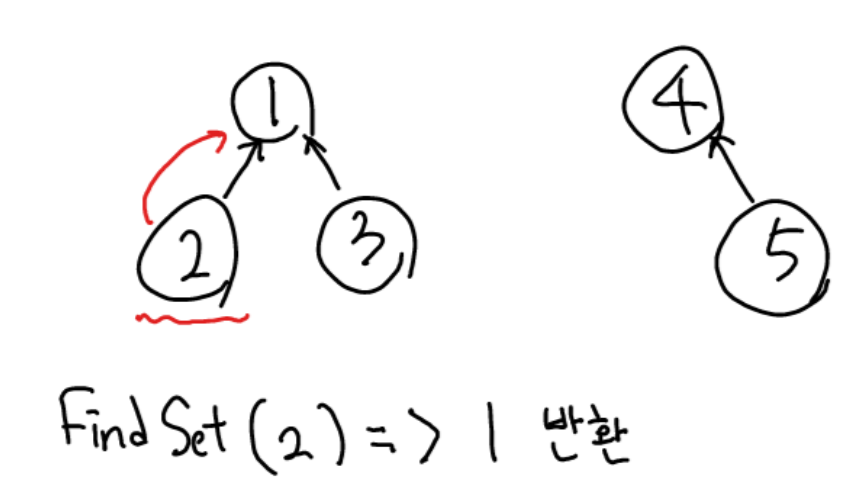
2. Find-Set

특정 요소가 속한 집합을 찾는 연산.
가장 최상단의 부모 노드를 찾아 반환하는 형태로 구현된다.
이를 통해 두 노드가 서로 같은 부모를 공유하면 같은 집합에 속한 것이고,
다른 부모를 가진다면 서로 다른 집합에 속한 것임을 알 수 있다.

 

 

 

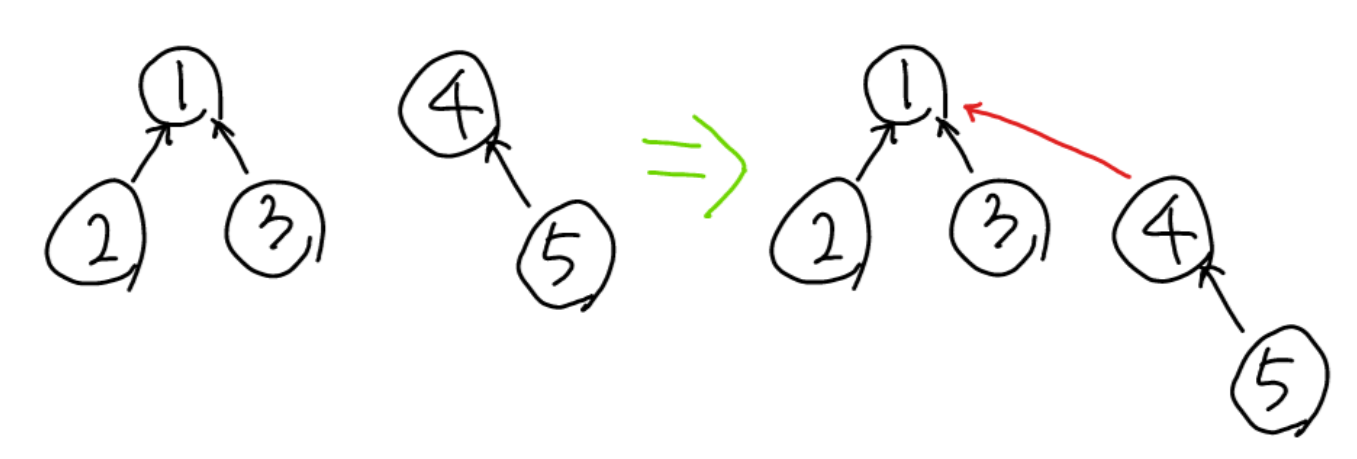
3. Union

두 집합을 하나로 병합하는 연산.

 

 

BFS가 필요한 상황?

1. 그래프의 연결 여부 판단: 그래프 노드가 연결되어있는지 판단할 수 있다. 최소신장트리 알고리즘 등에서 사용된다.

 

2. 사이클 검사 : 무방향 그래프에서 사이클이 있는지 여부를 확인할 때 사용

 

 

장점

• 집합 관리에 효율적이다. 시간복잡도가 거의 상수 시간에 가까워진다.
  
  
• 크루스칼 알고리즘과 같은 최소 신장 트리 알고리즘에서 그래프의 연결성 관리하는 데 필수적이다.

 

단점

• 새로운 요소를 추가하는 연산이 없어 고정된 집합에서만 사용 가능
  
  
• 트리 구조로 관리하는 형태이기 때문에, 트리 높이를 효율적으로 유지하기 위한 추가적 연산 필요

 

 

 

구현

public class DisjointSetArray {

    // Make-Set: 각 원소가 자신을 부모로 갖는 새로운 집합을 생성
    public static void makeSet(int[] parent, int[] rank, int n) {
        for (int i = 0; i < n; i++) {
            parent[i] = i;  // 자신이 부모
            rank[i] = 0;    // 초기 랭크는 0
        }
    }

    // Find-Set: x가 속한 집합의 루트(대표자)를 찾음, 경로 압축 적용
    public static int findSet(int[] parent, int x) {
        if (parent[x] != x) {
            parent[x] = findSet(parent, parent[x]);  // 경로 압축
        }
        return parent[x];
    }

    // Union: 두 집합을 병합, 랭크를 기준으로 병합
    public static void union(int[] parent, int[] rank, int x, int y) {
        int rootX = findSet(parent, x);
        int rootY = findSet(parent, y);

        if (rootX != rootY) {
            // 랭크를 기준으로 작은 트리를 큰 트리 밑에 붙임
            if (rank[rootX] > rank[rootY]) {
                parent[rootY] = rootX;  // rootY를 rootX에 병합
            } else if (rank[rootX] < rank[rootY]) {
                parent[rootX] = rootY;  // rootX를 rootY에 병합
            } else {
                parent[rootY] = rootX;  // 둘의 랭크가 같을 때
                rank[rootX]++;          // rootX의 랭크 증가
            }
        }
    }

    public static void main(String[] args) {
        int n = 5; // 5개의 원소
        int[] parent = new int[n];  // 부모 배열
        int[] rank = new int[n];    // 랭크 배열

        // Make-Set: 5개의 원소 각각을 독립적인 집합으로 생성
        makeSet(parent, rank, n);

        // Union 연산: 1과 2를 병합, 3과 4를 병합, 2와 3을 병합
        union(parent, rank, 1, 2);
        union(parent, rank, 3, 4);
        union(parent, rank, 2, 3);

        // Find-Set 연산: 1과 4가 같은 집합에 속하는지 확인
        if (findSet(parent, 1) == findSet(parent, 4)) {
            System.out.println("1과 4는 같은 집합에 속합니다.");
        } else {
            System.out.println("1과 4는 다른 집합에 속합니다.");
        }

        // Find-Set 연산: 5는 어느 집합에 속하는지 확인
        System.out.println("5의 대표: " + findSet(parent, 4));
    }
}