백준 1806: 부분합
문제 설명
10,000 이하의 자연수로 이루어진 길이 N짜리 수열이 주어진다. 이 수열에서 연속된 수들의 부분합 중에 그 합이 S 이상이
되는 것 중, 가장 짧은 것의 길이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N (10 ≤ N < 100,000)과 S (0 < S ≤ 100,000,000)가 주어진다. 둘째 줄에는 수열이 주어진다. 수열의 각 원소는
공백으로 구분되어져 있으며, 10,000이하의 자연수이다.
출력
첫째 줄에 구하고자 하는 최소의 길이를 출력한다.
만일 그러한 합을 만드는 것이 불가능하다면 0을 출력하면 된다.
제출 코드
1. 시간 초과수열을 입력받으면서, 누적합을 저장하는 배열을 추가로 만들어 누적합을 저장했다.
모든 배열의 합을 일일이 구하지 않아도 누적합에서 빼기 한번으로 부분합을 구할 수 있도록 하기 위함이었다.
(예)
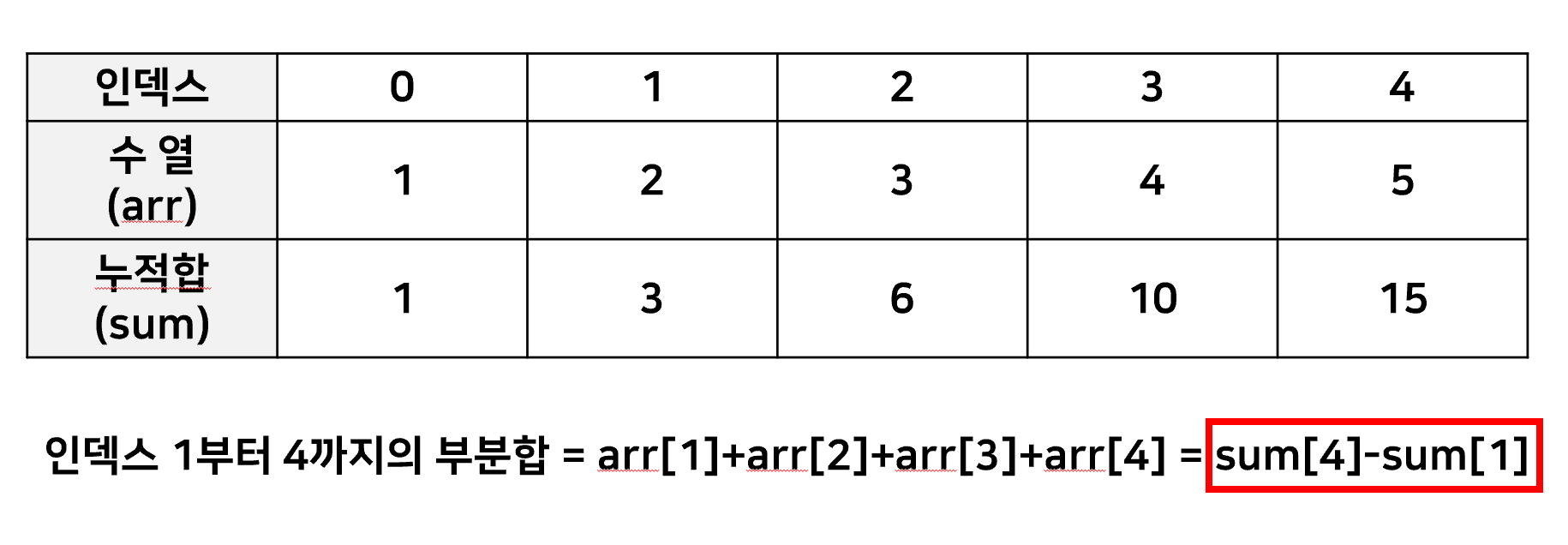
하지만, 이 또한 N개의 인덱스 중 2개를 뽑아 조합하는 경우의 수만큼 작업이 수행되므로,
100000 C 2 = 약 50억 가량의 작업이 소요될 수 있어 시간이 초과하였다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int S = Integer.parseInt(st.nextToken());
int[] arr = new int[N+1];
int[] sum = new int[N+1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
sum[i] = sum[i - 1] + arr[i];
}
if (S <= 0) {
System.out.println(0);
return;
}
// 부분합 수열의 개수
for (int n=1; n<=N; n++) {
for (int start=1; start<=N-n; start++) {
if (sum[start+n]-sum[start] >= S) {
System.out.println(n);
return;
}
}
}
System.out.println(0);
}
}
2. 성공
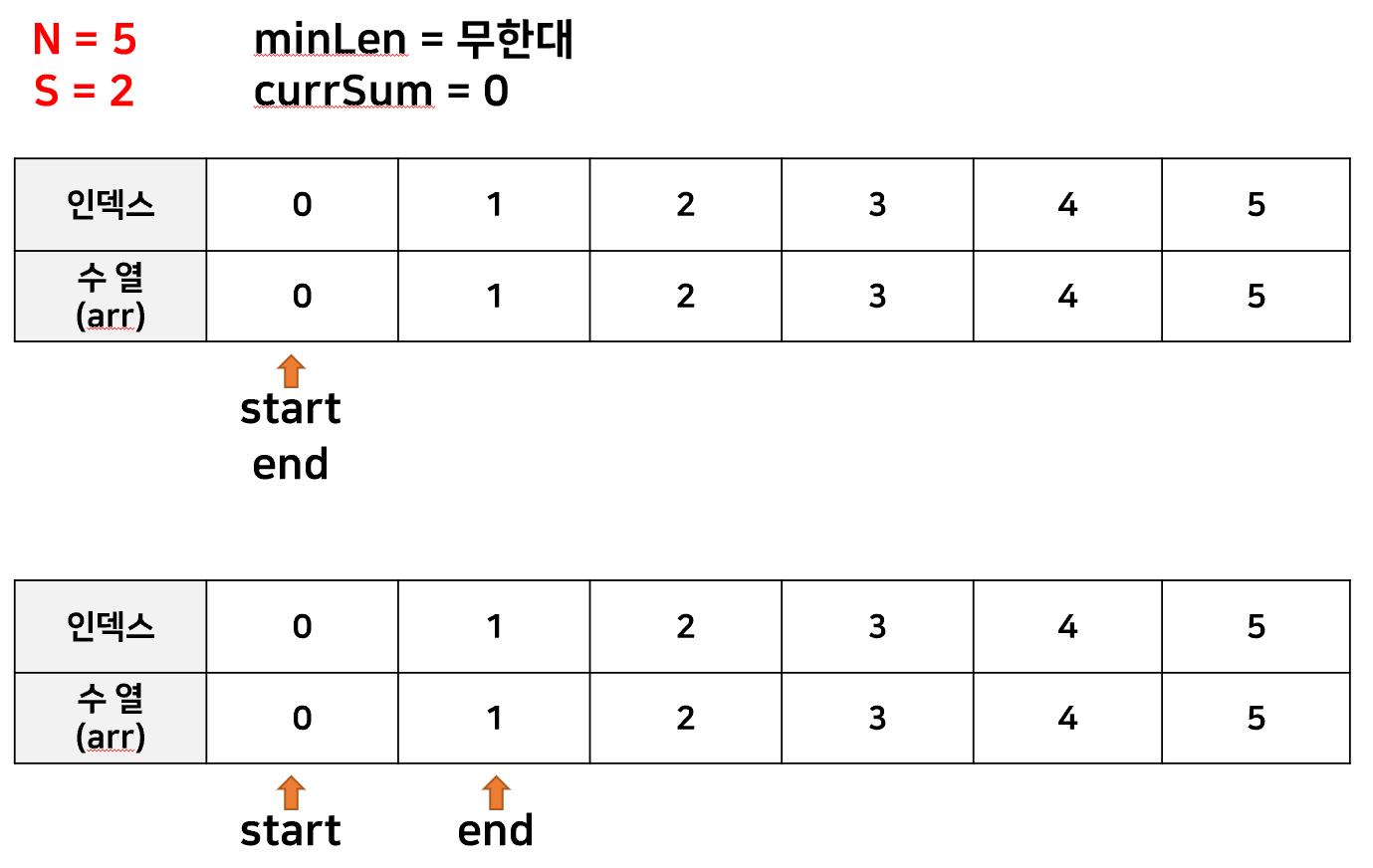
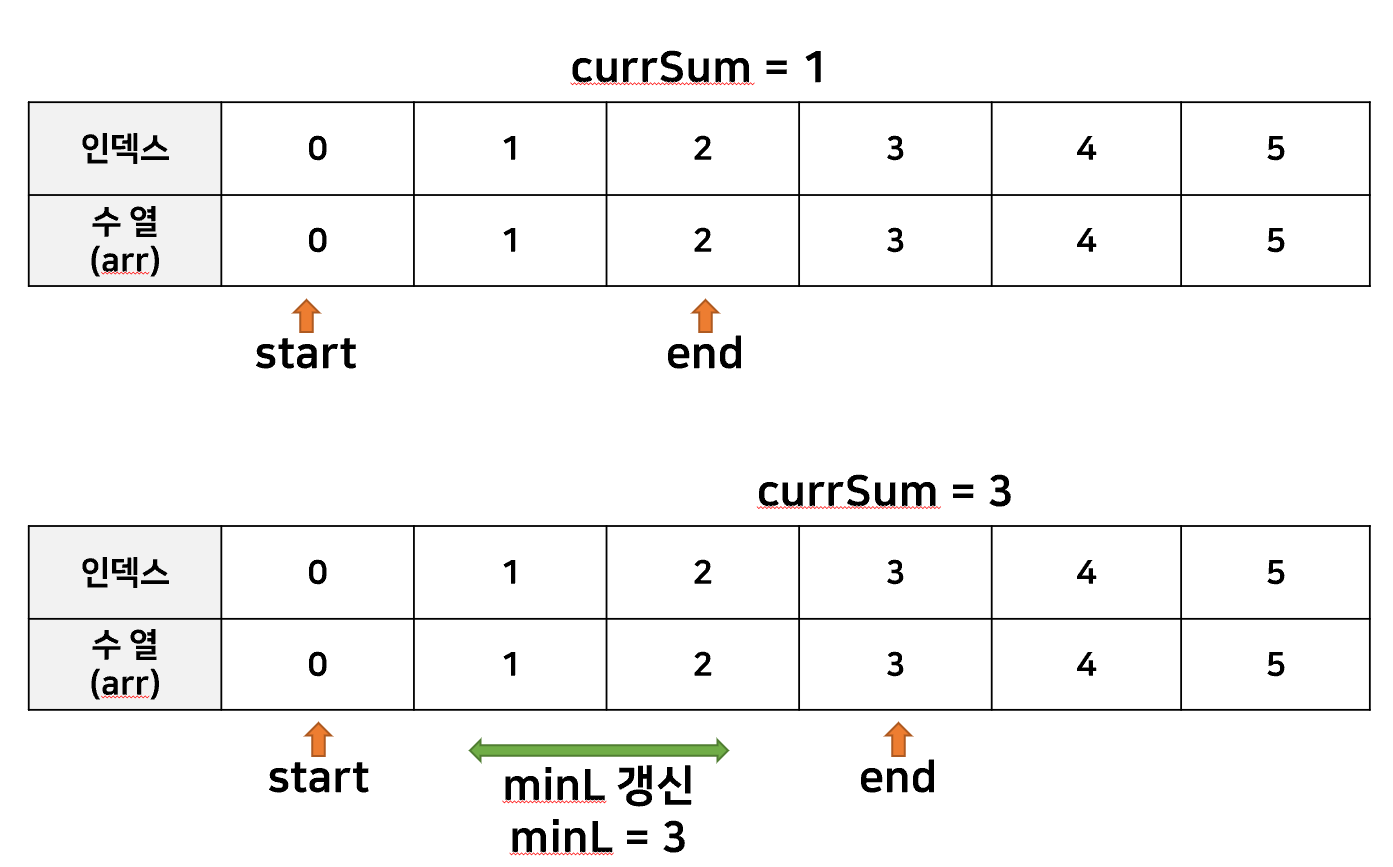
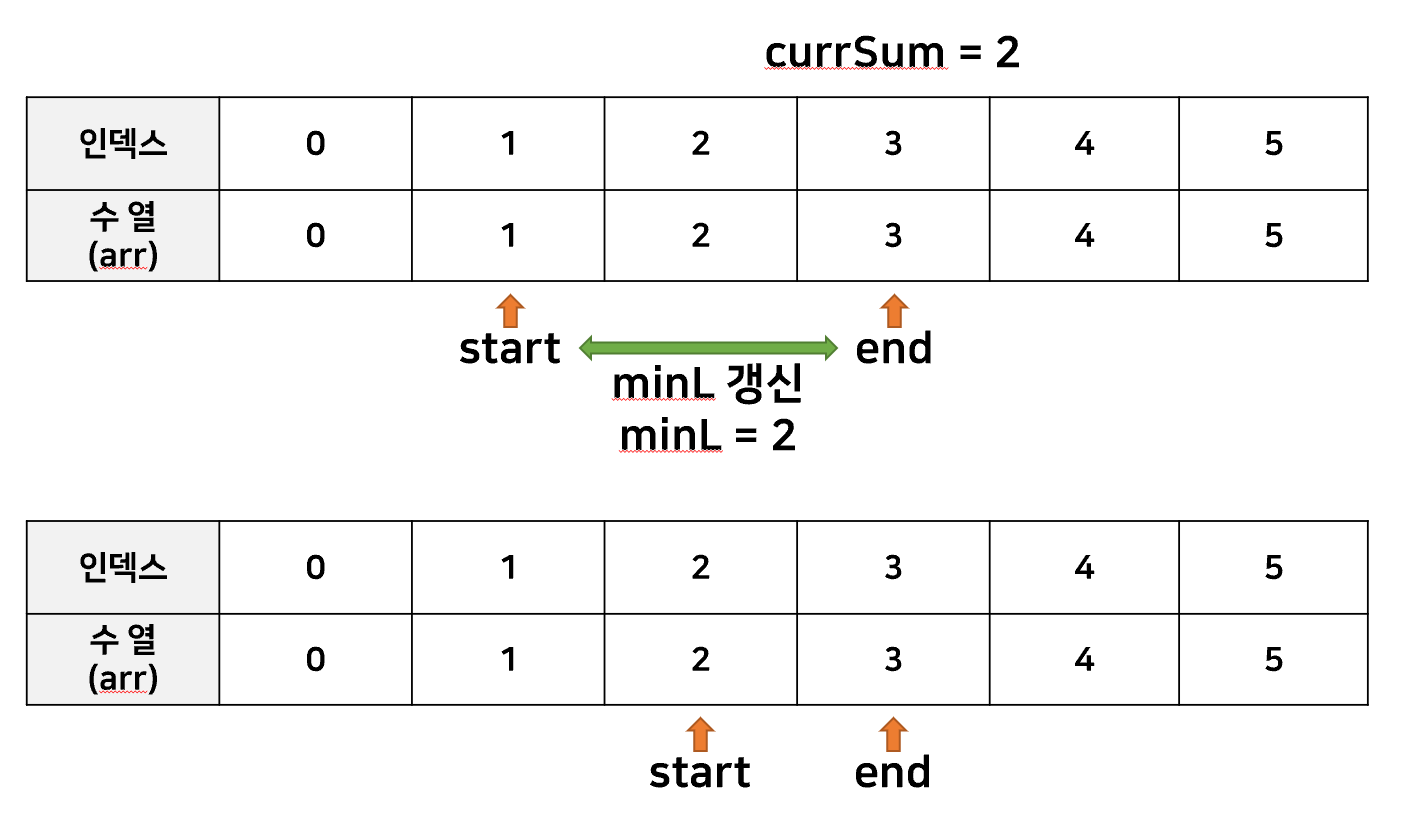
start 포인터와 end 포인터를 각각 선언하여
두 포인터의 위치를 조금씩 조정해가며 최소 개수의 수열을 구하는 방법이 있었다.
이 방법을 사용하면, end포인터와 start포인터 각각 움직이더라도 배열을 1번만 순회하므로
O(n)의 시간복잡도를 가진다고 할 수 있다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int S = Integer.parseInt(st.nextToken());
int[] arr = new int[N+2];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int start = 0;
int end = 0;
int minL = Integer.MAX_VALUE;
int currSum = 0;
while(end <= N+1 && start <= N) {
if (currSum < S) {
currSum += arr[end++];
}
else {
minL = Math.min(minL, end-start);
currSum -= arr[start++];
}
}
if (minL == Integer.MAX_VALUE) {
System.out.println(0);
} else {
System.out.println(minL);
}
}
}
