문제 설명
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다.
이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
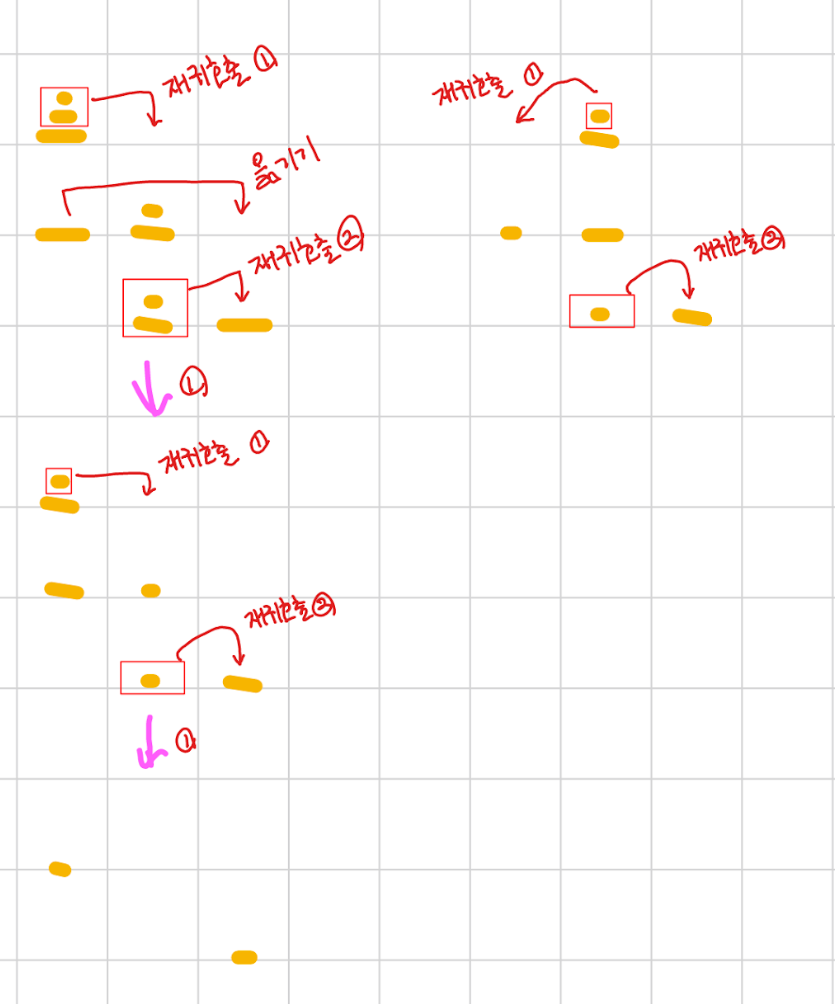
아래 그림은 원판이 5개인 경우의 예시이다.

입력
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
출력
첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데,
이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.
제출 코드(실패)
Stack OverFlow가 발생했다.
특정 규칙을 찾아보려 했으나 찾지 못해 완전 탐색 방식을 사용했다.
한번의 재귀함수 호출에서 5가지 경우의 수로 뻗어 나가다 보니
5의 지수만큼 스택에 쌓여 순식간에 오버플로우가 발생했다.
문제 해결 방법을 다시 생각해야 했다.
public class Main {
static int N, min;
static Stack<Integer>[] towers;
static String result;
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
min = Integer.MAX_VALUE;
result = "";
// 장대 3개, 최대 높이 N개의 탑
towers = new Stack[3];
for (int i=0; i<3; i++) {
towers[i] = new Stack<>();
}
for (int i = N; i >= 1; i--) {
towers[0].push(i);
}
dfs(0, 0, 0, new StringBuilder());
System.out.println(min);
System.out.println(result);
}
private static void dfs(int count, int prevPop, int prevPush, StringBuilder route) {
System.out.println(prevPop+"에서 "+prevPush+"로 이동 " + towers[0]+" | "+towers[1]+" | "+towers[2]);
if (towers[2].size() >= N) {
if (min > count) {
min = count;
result = route.toString();
}
return;
}
int length = route.length();
// i번 타워에서 j번 타워로 옮기기
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (i==j) continue;
// 이전 이동과 반대되는 이동(왔다갔다)은 PASS
if (prevPush == i && prevPop == j) continue;
if (towers[i].size() <= 0) continue;
if (towers[j].size() == 0 || towers[j].peek() > towers[i].peek()) {
moveDisk(i, j); // 옮기기
route.append(i).append(' ').append(j).append('\n');
dfs(count + 1, i, j, route); // 재귀함수 호출
moveDisk(j, i); // 원상복구
route.delete(length, route.length()-1);
}
}
}
}
private static void moveDisk(int popTower, int pushTower) {
int popDisk = towers[popTower].pop();
towers[pushTower].push(popDisk);
}
}
개선 코드
public class Main {
static int N, moveCount;
static Stack<Integer>[] towers;
static StringBuilder result;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
moveCount = 0;
result = new StringBuilder();
moveDisks(N, 1, 3, 2);
System.out.println(moveCount);
System.out.println(result);
}
private static void moveDisks(int diskCount, int start, int end, int sub) {
if (diskCount == 1) {
moveCount += 1;
result.append(start).append(' ').append(end).append('\n');
return;
}
// 보조기둥으로 diskCount-1개만큼 옮기기
moveDisks(diskCount - 1, start, sub, end);
// 남은 1개 원판을 목표기둥으로 옮기기
moveCount += 1;
result.append(start).append(' ').append(end).append('\n');
// 보조기둥의 원판들을 목표기둥으로 옮기기
moveDisks(diskCount - 1, sub, end, start);
}
}
문제를 작은 문제로 쪼개야 했다.
문제 해결을 위한 로직은 아래와 같다.
1. N-1개의 원판을 보조기둥으로 옮긴다.
2. 남은 1개의 원판을 목표 기둥으로 옮긴다.
3. 보조기둥에 있는 N-1개의 원판을 목표 기둥으로 옮긴다.
로직을 재귀함수 호출 방식으로 N이 1이 될 때까지 잘게 쪼개 문제를 해결한다.
깨달은 점
나름 충격적인 풀이법이었다.
이 문제의 해결 방식을 보고
문제를 작은 단위로 쪼개 문제를 해결하는 분할 정복의 느낌을 많이 받았는데,
문제를 가능한 간단한 해결 방법을 생각하는 것, 작은 단위로 쪼개 생각하는 능력을 기르는 훈련이 필요함을 느꼈다.
