백준 1676: 팩토리얼 0의 개수
문제 설명
N!에서 뒤에서부터 처음 0이 아닌 숫자가 나올 때까지 0의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (0 ≤ N ≤ 500)
출력
첫째 줄에 구한 0의 개수를 출력한다.
제출 코드
실행속도 : 64ms
메모리 : 11512KB

숫자 끝에 0이 붙으려면 어떤 수에 10을 곱해야 한다는 것이 포인트
그렇다면, 팩토리얼 에서 10이 곱해지는 경우는 2*5뿐이다 (10도 2*5 쌍이라고 볼 수 있다)
따라서 N!에서 끝 0의 개수는?
1부터 N까지 모든 수를 소인수분해했을 때 2,5 짝의 개수를 구하면 됨.
여기서 2의 개수는 2, 4, 8 ... 로 5의 개수보다 확실히 많으므로,
=> 결국 5의 개수를 세면 된다!
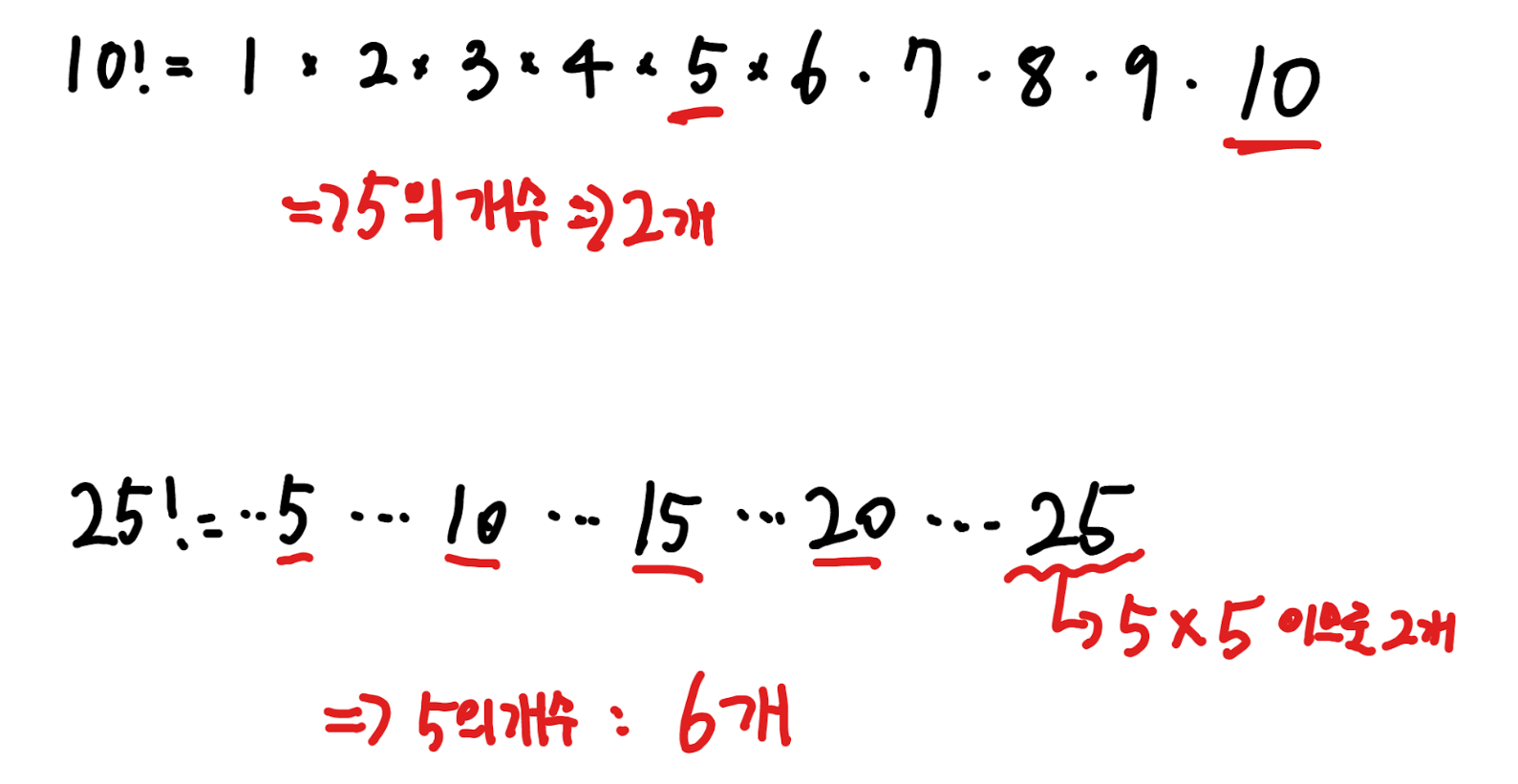
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Scanner;
import java.util.Stack;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int zeroCount = 0;
for (int i=5; i<=N; i+=5) {
// 5로 나눠지는 횟수만큼 0 개수 추가
zeroCount += countFive(i);
}
System.out.println(zeroCount);
}
private static int countFive(int i) {
int count = 0;
while (i % 5 == 0) {
i /= 5;
count += 1;
}
return count;
}
}
5의 개수만 세면 되므로, 5부터 N까지 i를 5씩 증가시키며 5의 배수일 때만
countFive 메서드를 만들어 5의 수를 세었다.
개선 코드
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int zeroCount = 0;
// 5의 배수마다 5의 개수를 더함
for (int i = 5; i <= n; i *= 5) {
zeroCount += n / i;
}
System.out.println(zeroCount);
}
}
- i를 5씩 증가시키는 대신, 5의 제곱 배수를 한 번에 처리했다.
이를 통해 5, 25, 125 등에서 각각 추가로 생기는 5의 개수를 누적할 수 있다. - 기존 코드는 i를 5씩 증가시켜 시간복잡도가 O(N/5* log₅N) 인 반면,
이 방식은 i를 5씩 곱해주며 시간 복잡도를 O(log₅N)으로 최적화할 수 있었다!
깨달은 점
기존 코드도 충분히 효율적인 코드라고 느껴져 더 개선할 점이 있을까 생각했는데,
5의 개수를 구하는 과정에서 5의 지수마다 변곡점이 생기므로, 5씩 곱해주며 계산할 수 있는 방법이 있다는 것에 놀랐다.
언제나 더 효율적인 코드는 존재한 다는 것을 다시 한번 느낀다.
