플로이드워셜 알고리즘에 대해 공부했지만,
항상 다익스트라를 써야할 지, 플로이드워셜 알고리즘을 써야할 지 고민하다가 다익스트라를 사용해왔다.
하지만 특정 상황에서는 플로이드워셜 알고리즘이 훨씬 효율적이라는 것..
확실히 기억해두자.
문제는 백준 14938번 "서강그라운드" 를 가지고 풀어보겠다.
간단 요약하면, 가중치가 다른 양방향 간선 그래프가 주어지고, 각 노드별로 가중치가 주어진다. 여기서 거리가 M 이내인 모든 노드들의 가중치 총합의 최대값을 찾는 문제이다.
여기서 문제 풀이 핵심은, 임의 노드 i에서 j로 가는 모든 노드의 최단거리를 각각 구하는 것이다.
이 때, i에서 j로 가는 직행 루트가 없을 수 있기도 하고, 직행 루트보다 다른 곳을 거쳐 가는게 더 저렴할 수도 있기 때문에!!
(1) 플로이드 워셜 알고리즘을 쓰거나, (2) 다익스트라 알고리즘을 사용해 최단거리를 찾아야 한다.
로직 흐름
(1) 플로이드 워셜 알고리즘
- dist[i][j] 배열을 초기화한다. (자기 자신은 0, 직접 연결된 간선은 가중치, 없으면 무한대)
- 중간에 거칠 수 있는 노드를 하나씩 선택하면서, 거쳐가는 경로가 더 짧으면 갱신한다.
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]) - k를 1부터 N까지 늘려가며, 경유 가능한 노드 집합을 확장한다.
- k=1일 때: 노드 1을 경유해서 가는 모든 경로 최단거리 갱신
- k=2일 때: 노드 1 또는 2를 경유해서 가는 경로 최단거리 갱신
- 이를 반복하면 모든 쌍의 최단거리가 완성된다.
(2) 다익스트라 알고리즘
- dist[start] = 0으로 설정하고, 나머지는 무한대로 초기화한다.
- 방문하지 않은 노드 중 가장 거리가 짧은 노드를 선택한다.
- 해당 노드의 모든 인접 노드에 대해, 현재노드까지의 거리 + 간선 가중치가 더 짧으면 갱신한다.
- 모든 노드를 방문할 때까지 2~3 과정을 반복한다.
예를 들어 노드 5개, 시작 노드 1일 때의 dist 초기 상태는 다음과 같다.
- 1번 방문 → 2번과 4번 거리 갱신
- 다음으로 거리가 짧은 2번 방문 → 3번 거리 갱신
- 다음으로 4번 방문 → 5번 거리 갱신
- 이런 식으로 한 시작점에서의 최단거리를 완성한다.
시간복잡도
플로이드 워셜 : for문을 3번 돌기 때문에, O(N^3) 이다.
다익스트라 : 간선 수가 E라고 할 때, O(E logN)가 된다.
따라서 간선 수가 많을 수록 다익스트라는 불리해지고,
노드 수가 많을수록 플로이드 워셜이 불리해진다.
백준 14938 문제 예시 코드
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StringBuilder sb = new StringBuilder();
static int N, M, R, max;
static final int INF = Integer.MAX_VALUE;
static int[] items;
static int[][] dist;
static int[][] dist_dijkstra;
static ArrayList<Site>[] adjList;
static class Site {
int v;
int l;
public Site(int v, int l) {
super();
this.v = v;
this.l = l;
}
}
public static void main(String[] args) throws IOException {
init();
long start = System.currentTimeMillis();
// 플로이드 워셜
floydWarshall();
// 다익스트라
dijkstra();
// 낙하위치별 최단거리 구하기
max = 0;
for (int i=1; i<=N; i++) {
int sum = items[i];
for (int j=1; j<=N; j++) {
if (i==j) continue;
if (dist_dijkstra[i][j] <= M) {
// if (dist[i][j] <= M) {
sum += items[j];
}
}
max = Math.max(max, sum);
}
System.out.println(max);
long end= System.currentTimeMillis();
System.out.println(end - start);
}
private static void floydWarshall() {
// i에서 j로 가는 모든 경로에서 k를 거쳐갈 때 최단거리
// 양방향 통행 => (i>j) == (j>i) 이므로 중복 계산 줄임
for (int k=1; k<=N; k++) {
for (int i=1; i<=N; i++) {
if (dist[i][k] == INF) continue;
for (int j=i+1; j<=N; j++) {
if (i==j) continue;
if (dist[k][j] == INF) continue;
if (dist[i][j] > dist[i][k]+dist[k][j]) {
dist[i][j] = dist[i][k]+dist[k][j];
dist[j][i] = dist[i][j];
}
}
}
}
}
static void dijkstra() {
dist_dijkstra = new int[N + 1][N + 1];
final int INF = Integer.MAX_VALUE;
for (int s = 1; s <= N; s++) {
Arrays.fill(dist_dijkstra[s], INF);
dist_dijkstra[s][s] = 0;
// (정점, 현재까지의 거리)로 사용
java.util.PriorityQueue<Site> pq = new java.util.PriorityQueue<>((a, b) -> Integer.compare(a.l, b.l));
pq.offer(new Site(s, 0));
while (!pq.isEmpty()) {
Site cur = pq.poll();
int u = cur.v;
int d = cur.l;
// 이미 더 짧은 경로가 있으면 스킵
if (d > dist_dijkstra[s][u]) continue;
// 인접 정점 완화
for (Site nx : adjList[u]) {
int v = nx.v;
int w = nx.l;
// d + w 연산 전 INF 가드 (오버플로 방지용)
if (d != INF && d + w < dist_dijkstra[s][v]) {
dist_dijkstra[s][v] = d + w;
pq.offer(new Site(v, dist_dijkstra[s][v]));
}
}
}
}
}
private static void init() throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
R = Integer.parseInt(st.nextToken());
items = new int[N+1];
adjList = new ArrayList[N+1];
for (int i=1; i<=N; i++) {
adjList[i] = new ArrayList<>();
}
// 지역별 아이템 수 입력
st= new StringTokenizer(br.readLine());
for (int i=1; i<=N; i++) {
items[i] = Integer.parseInt(st.nextToken());
}
// 플로이드 워셜용 배열
dist = new int[N+1][N+1];
for (int i=1; i<=N; i++) {
for (int j=1; j<=N; j++) {
if (i==j) continue;
dist[i][j] = INF;
}
}
// 인접 정보 리스트 입력
for (int i=1; i<=R; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int l = Integer.parseInt(st.nextToken());
dist[a][b] = l;
dist[b][a] = l;
adjList[a].add(new Site(b, l));
adjList[b].add(new Site(a, l));
}
}
}
코드가 긴데, 플로이드 워셜과 다익스트라를 모두 구현해놓아서 그렇다.
주석 처리를 통해 시간을 비교할 수 있도록 코드를 작성해봤다.
문제에서는 범위가 N이 100 이내이고, 간선도 100 이내라서, 실행시간의 큰 차이를 보이지 않았다.

위가 다익스트라, 아래가 플로이드 워셜이다.
그래서,
N 범위를 더 크게 해서 테스트케이스를 만들어 실험해봤다!
테스트케이스는 GPT를 활용해 테스트케이스를 만드는 파이썬 코드를 생성하여 적용했다.
속도 비교 실험
1-1. 노드 수 :500개, 간선 수:120000개
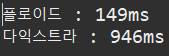
1-2. 노드 수: 500개, 간선 수 : 60000개

1-3. 노드 수: 500개, 간선 수: 10000개

=> 간선 수가 줄어들수록 확실히 다익스트라는 빨라진다!!
=> 반면, 플로이드는 약간 느려졌는데, 큰 의미는 없는 수치로 보인다.
2-1. 노드 수: 1000개, 간선 수: 490000개

2-2. 노드 수: 1000개, 간선 수: 245000개
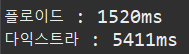
2-3. 노드 수: 1000개, 간선 수:100000개

2-4. 노드 수: 1000개, 간선 수:10000개

=> 플로이드는 O(N^3) 이므로 노드 수 500에 비해 이론상 10배 이상 실행시간이 늘어야 한다. 결과를 보면 얼추 10배 정도 나온 것으로 보인다.
=> 다익스트라는 간선 수에 비례하게 속도가 빨라지는 것으로 보인다. 노드수 500에 비해서는 이론 상 1.1배 실행시간 늘어나야 하는데, 244 -> 621이면 꽤 많이 늘어난 것 같다.
결론!!
모든 노드 간 최단 거리를 구해야 할 때, 노드 수 500까지는 웬만하면 플로이드 워셜이 빠르다.
다익스트라가 더 빨라지는 구간은 노드 수가 1000 이상쯤부터. 다만 간선 수가 매우 적어야 한다. 완전 그래프 N*(N-1)/2 에 비해 현저히 작아야 다익스트라가 유리해진다!!
