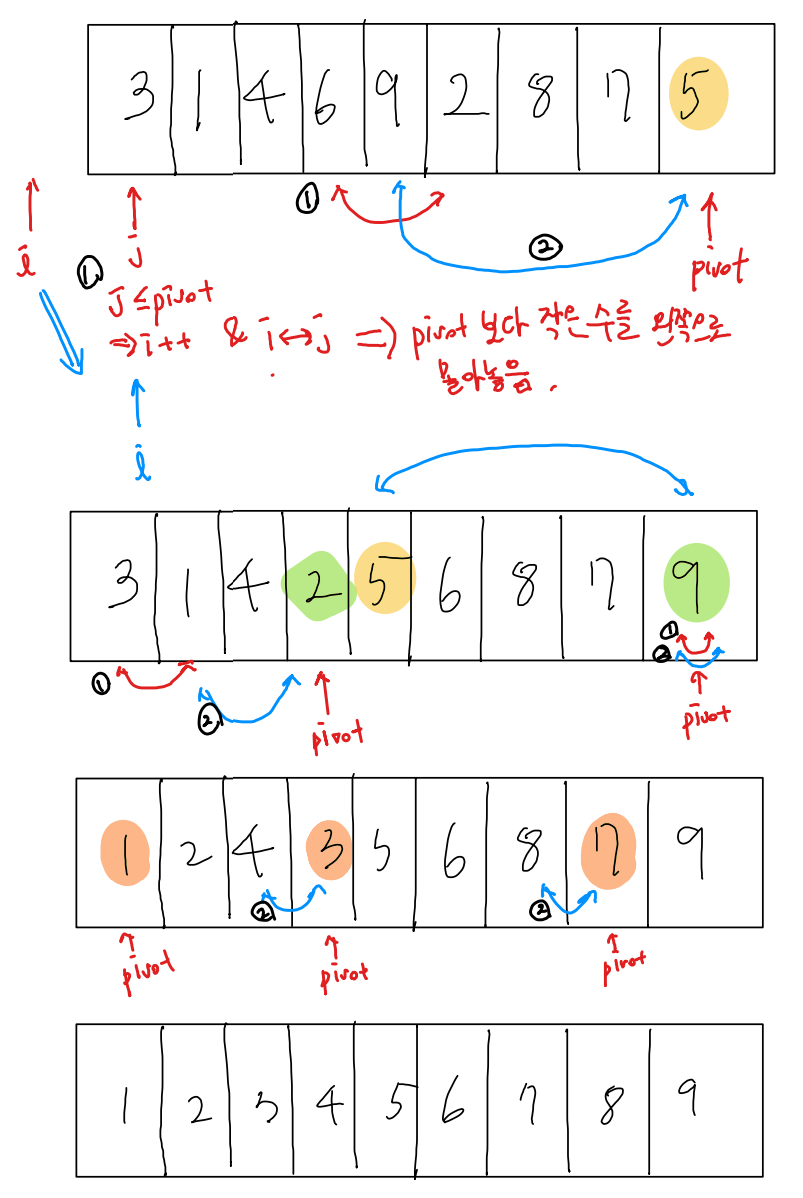
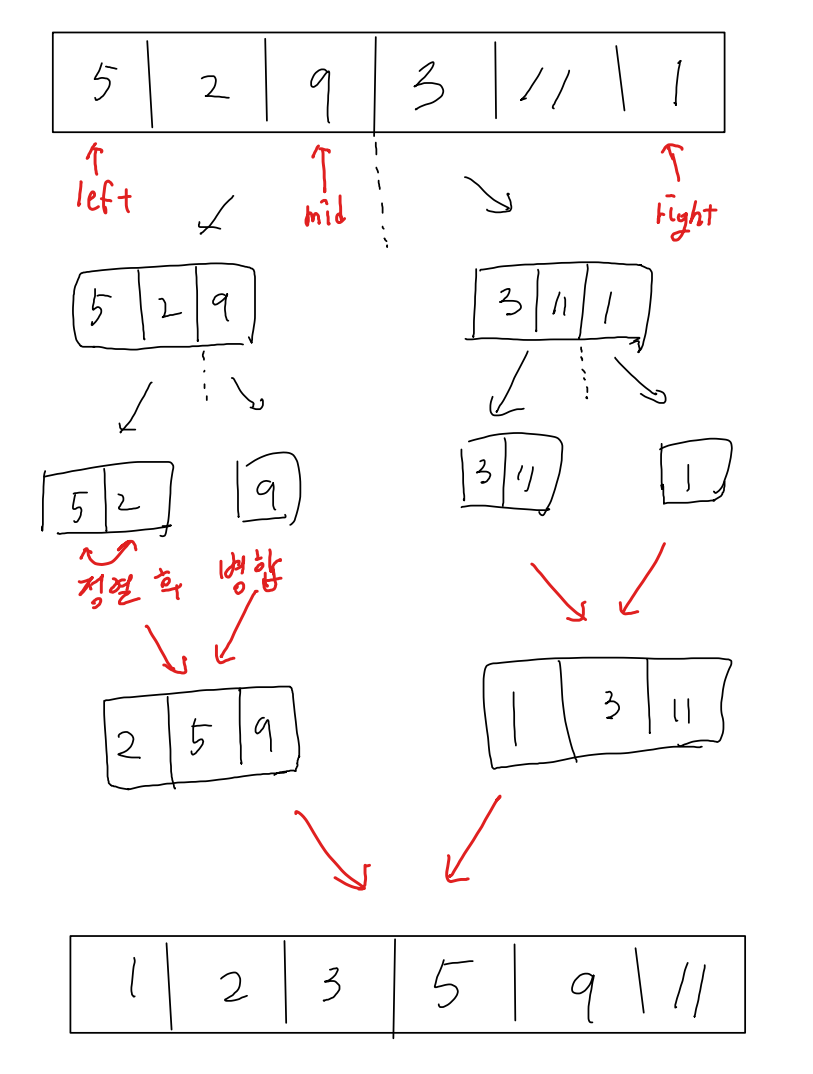
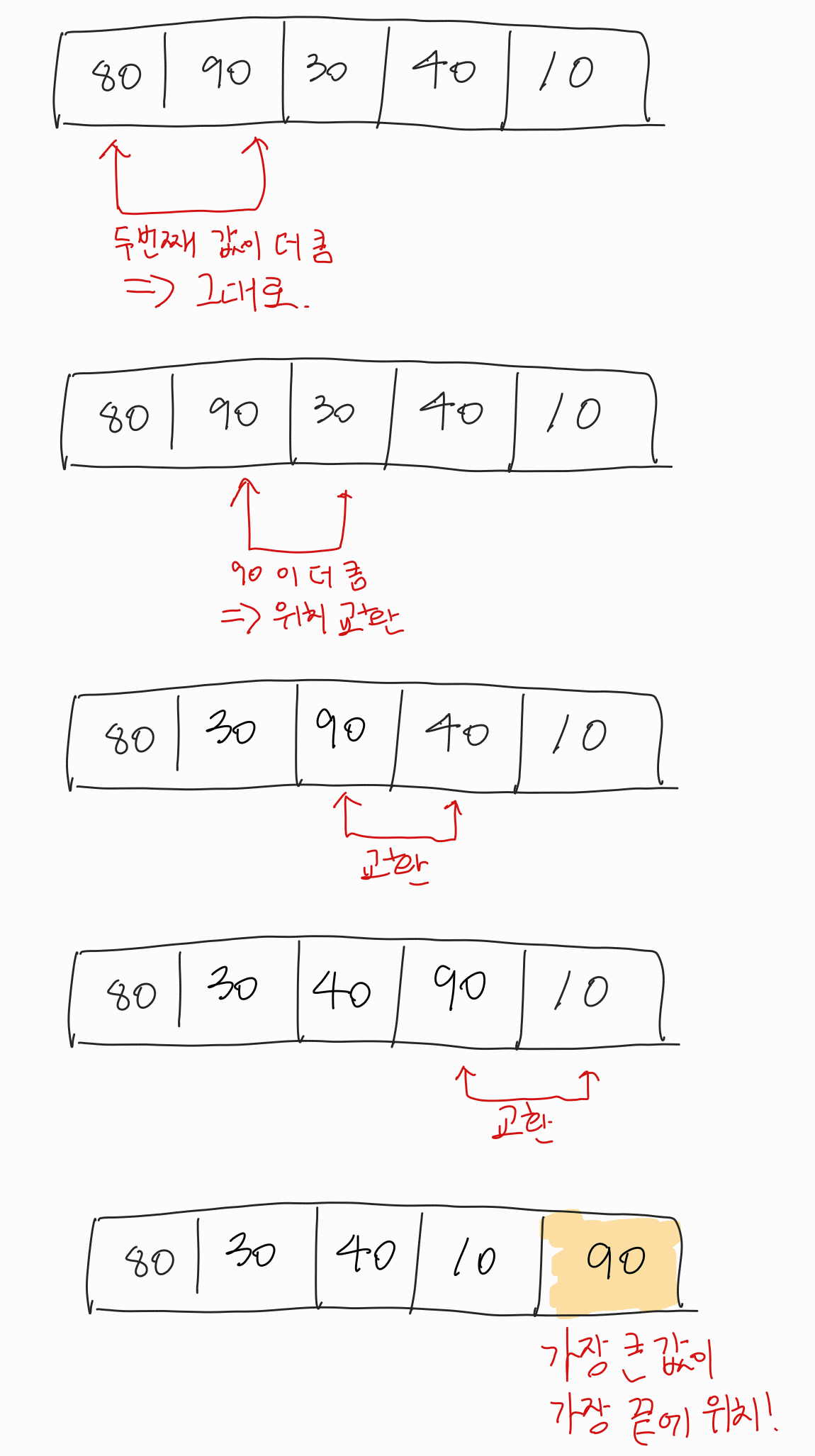
깊이우선탐색 (DFS)
- Depth-First Search
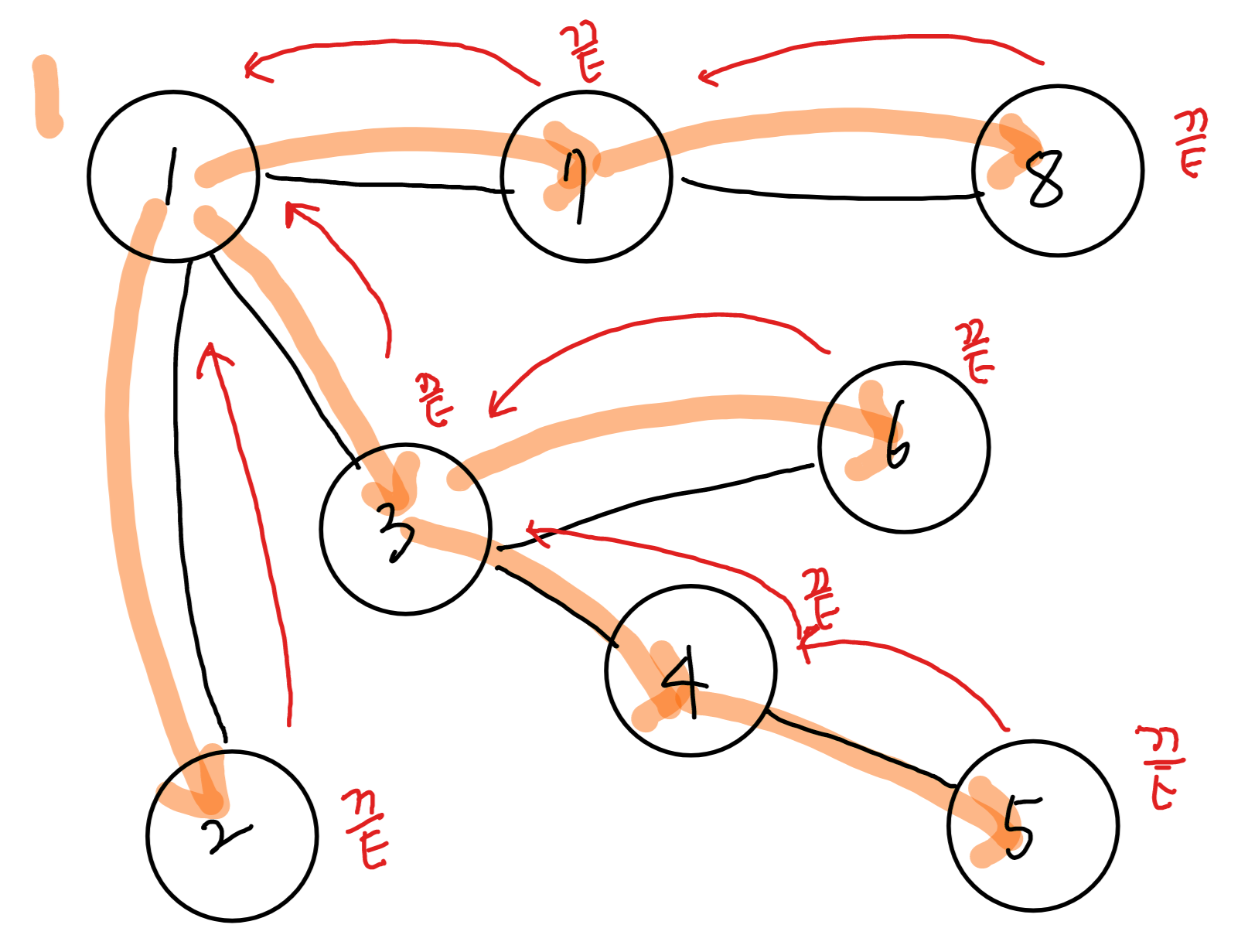
- 그래프 or 트리에서 한 노드 지정해 탐색을 시작, 인접한 노드를 탐색하고 더 깊은 단계로 들어가며 탐색을 이어나감
- 한 경로를 끝까지 탐색한 후 다음 경로로 넘어간다
동작 원리
- 시작 노드에서 출발하여 가장 깊은 노드까지 탐색을 진행
- 더이상 방문할 노드가 없으면, 한 단계 위로 돌아가서 탐색을 이어나감
- 모든 노드를 방문할 때까지 반복!
DFS가 필요한 상황?
1. 경로 탐색 문제 : 미로 탐색 등의 문제에서 특정 경로를 탐색해야 하는 경우
2. 연결 요소 탐색 : 그래프에서 특정 노드를 탐색해야 할 때, 모든 노드를 탐색해야 할 때
3. 백트래킹 : 퍼즐이나 조합을 탐색할 때 백트래킹 알고리즘의 기반이 되는 방식!
4. 사이클 탐지 : 순환 그래프의 경우 사이클의 여부를 탐지할 때 사용 가능
장점
- 메모리 효율성 : BFS 방식에 비해 메모리 소비가 적다. 특히 그래프가 넓은 경우 더 효율적이다
- 깊이가 중요한 문제에 적합함.
단점
- 최적 경로가 보장되지 않는다. 최단 경로를 찾기 위해선 BFS가 적합
- 방문여부를 체크하지 않으면 무한 루프가 발생할 수 있다.
구현
1. 스택을 이용한 구현
import java.util.*;
public class DFSStack {
// DFS 알고리즘을 스택을 이용해 구현한 코드
public static void dfsStack(Map<Integer, List<Integer>> graph, int startNode) {
Stack<Integer> stack = new Stack<>();
Set<Integer> visited = new HashSet<>();
// 시작 노드를 스택에 추가
stack.push(startNode);
while (!stack.isEmpty()) {
int node = stack.pop(); // 스택에서 노드를 꺼냄
if (!visited.contains(node)) {
visited.add(node); // 방문한 노드로 처리
System.out.print(node + " "); // 방문 순서 출력
// 인접 노드를 스택에 추가
for (int neighbor : graph.get(node)) {
if (!visited.contains(neighbor)) {
stack.push(neighbor);
}
}
}
}
}
public static void main(String[] args) {
// 그래프 초기화
Map<Integer, List<Integer>> graph = new HashMap<>();
graph.put(1, Arrays.asList(2, 3, 7));
graph.put(2, Arrays.asList(1));
graph.put(3, Arrays.asList(1, 4, 6));
graph.put(4, Arrays.asList(3));
graph.put(5, Arrays.asList(5));
graph.put(6, Arrays.asList(3));
graph.put(7, Arrays.asList(1));
graph.put(8, Arrays.asList(7));
System.out.println("DFS using stack:");
dfsStack(graph, 1); // 0번 노드에서 DFS 시작
}
}
2. 재귀를 이용한 구현
메서드 호출은 Java 자체에서 스택 방식으로 처리되므로, 이를 이용해 재귀함수를 만들어 구현하는 방법.
가장 많이 사용된다!
import java.util.*;
public class DFSStack {
// 재귀를 이용한 DFS
public static void dfsRecursive(Map<Integer, List<Integer>> graph, int node, Set<Integer> visited) {
// 노드를 방문하고 출력
visited.add(node);
System.out.print(node + " ");
// 인접 노드를 재귀적으로 방문
for (int neighbor : graph.get(node)) {
if (!visited.contains(neighbor)) {
dfsRecursive(graph, neighbor, visited);
}
}
}
public static void main(String[] args) {
// 그래프 초기화
Map<Integer, List<Integer>> graph = new HashMap<>();
graph.put(1, Arrays.asList(2, 3, 7));
graph.put(2, Arrays.asList(1));
graph.put(3, Arrays.asList(1, 4, 6));
graph.put(4, Arrays.asList(3));
graph.put(5, Arrays.asList(5));
graph.put(6, Arrays.asList(3));
graph.put(7, Arrays.asList(1));
graph.put(8, Arrays.asList(7));
System.out.println("DFS using stack:");
dfsStack(graph, 1); // 0번 노드에서 DFS 시작
}
}