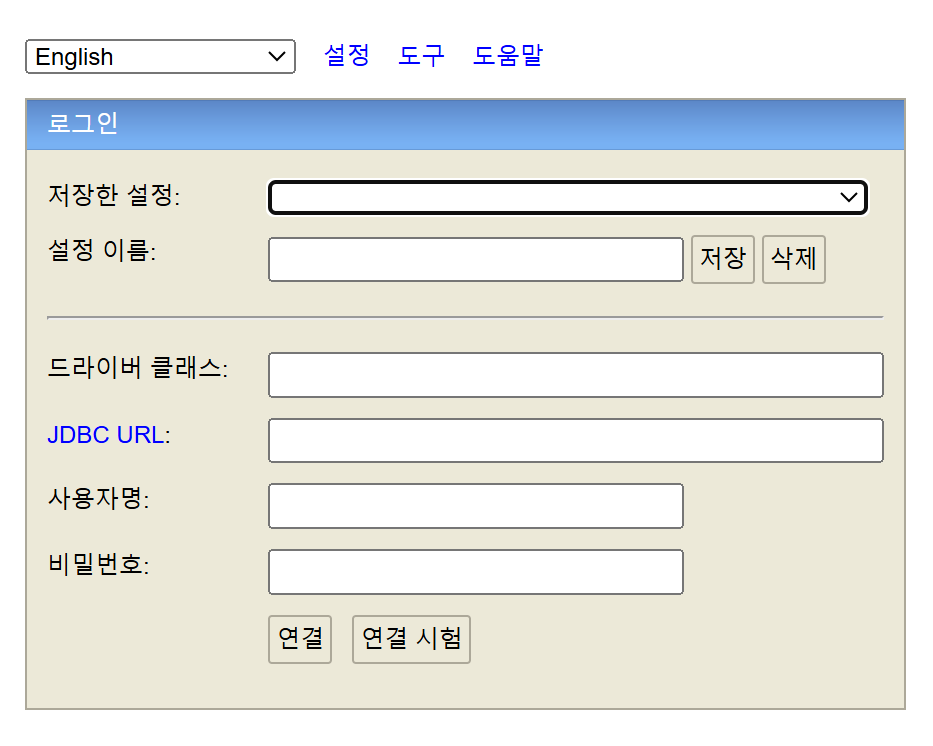
어느날 h2 데이터베이스를 실행했는데, 원래는 기본으로 저 입력란에 모두 영어로 뭐라뭐라 나와 있어야 하는데
모두 비어있었다.
도움말, 설정 다 둘러봤지만 도움은 안됨..
해결책은 간단하다

Setting Name: 부분에 Generic H2 (server)를 손수 입력해주면 뿅 하고 나타난다.
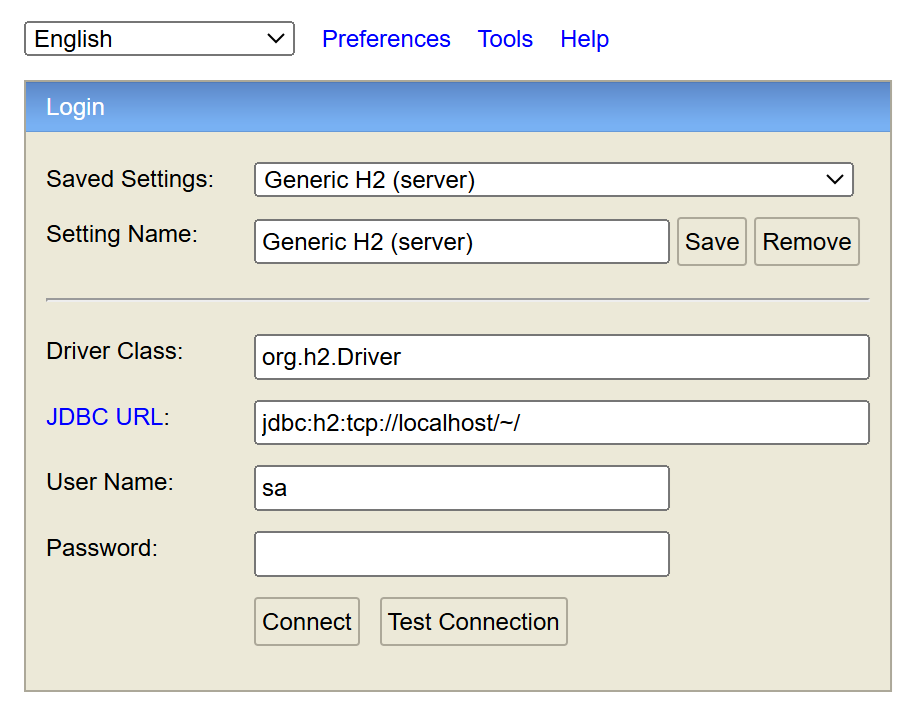
나머지 아래는 위와 같이 입력하면 된다. jdbc url 부분은 본인 데이터베이스 경로를 입력해준다.

어느날 h2 데이터베이스를 실행했는데, 원래는 기본으로 저 입력란에 모두 영어로 뭐라뭐라 나와 있어야 하는데
모두 비어있었다.
도움말, 설정 다 둘러봤지만 도움은 안됨..
해결책은 간단하다

Setting Name: 부분에 Generic H2 (server)를 손수 입력해주면 뿅 하고 나타난다.

나머지 아래는 위와 같이 입력하면 된다. jdbc url 부분은 본인 데이터베이스 경로를 입력해준다.
N!에서 뒤에서부터 처음 0이 아닌 숫자가 나올 때까지 0의 개수를 구하는 프로그램을 작성하시오.
첫째 줄에 N이 주어진다. (0 ≤ N ≤ 500)
첫째 줄에 구한 0의 개수를 출력한다.
실행속도 : 64ms
메모리 : 11512KB

숫자 끝에 0이 붙으려면 어떤 수에 10을 곱해야 한다는 것이 포인트
그렇다면, 팩토리얼 에서 10이 곱해지는 경우는 2*5뿐이다 (10도 2*5 쌍이라고 볼 수 있다)
따라서 N!에서 끝 0의 개수는?
1부터 N까지 모든 수를 소인수분해했을 때 2,5 짝의 개수를 구하면 됨.
여기서 2의 개수는 2, 4, 8 ... 로 5의 개수보다 확실히 많으므로,
=> 결국 5의 개수를 세면 된다!
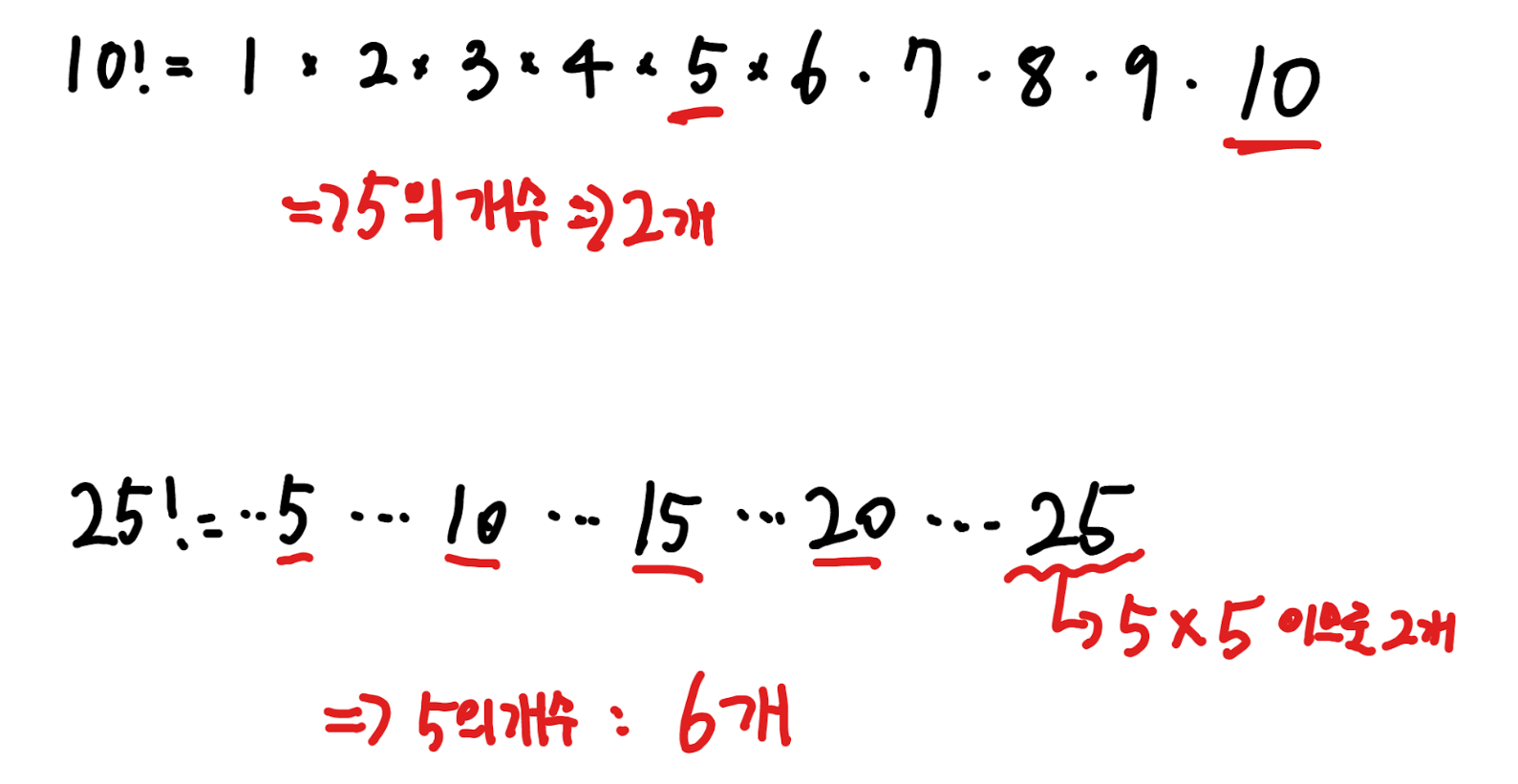
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Scanner;
import java.util.Stack;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int zeroCount = 0;
for (int i=5; i<=N; i+=5) {
// 5로 나눠지는 횟수만큼 0 개수 추가
zeroCount += countFive(i);
}
System.out.println(zeroCount);
}
private static int countFive(int i) {
int count = 0;
while (i % 5 == 0) {
i /= 5;
count += 1;
}
return count;
}
}
5의 개수만 세면 되므로, 5부터 N까지 i를 5씩 증가시키며 5의 배수일 때만
countFive 메서드를 만들어 5의 수를 세었다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int zeroCount = 0;
// 5의 배수마다 5의 개수를 더함
for (int i = 5; i <= n; i *= 5) {
zeroCount += n / i;
}
System.out.println(zeroCount);
}
}
기존 코드도 충분히 효율적인 코드라고 느껴져 더 개선할 점이 있을까 생각했는데,
5의 개수를 구하는 과정에서 5의 지수마다 변곡점이 생기므로, 5씩 곱해주며 계산할 수 있는 방법이 있다는 것에 놀랐다.
언제나 더 효율적인 코드는 존재한 다는 것을 다시 한번 느낀다.
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다.
이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.

첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
첫째 줄에 옮긴 횟수 K를 출력한다.
두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데,
이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다.
Stack OverFlow가 발생했다.
특정 규칙을 찾아보려 했으나 찾지 못해 완전 탐색 방식을 사용했다.
한번의 재귀함수 호출에서 5가지 경우의 수로 뻗어 나가다 보니
5의 지수만큼 스택에 쌓여 순식간에 오버플로우가 발생했다.
문제 해결 방법을 다시 생각해야 했다.
public class Main {
static int N, min;
static Stack<Integer>[] towers;
static String result;
public static void main(String[] args) throws IOException {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
min = Integer.MAX_VALUE;
result = "";
// 장대 3개, 최대 높이 N개의 탑
towers = new Stack[3];
for (int i=0; i<3; i++) {
towers[i] = new Stack<>();
}
for (int i = N; i >= 1; i--) {
towers[0].push(i);
}
dfs(0, 0, 0, new StringBuilder());
System.out.println(min);
System.out.println(result);
}
private static void dfs(int count, int prevPop, int prevPush, StringBuilder route) {
System.out.println(prevPop+"에서 "+prevPush+"로 이동 " + towers[0]+" | "+towers[1]+" | "+towers[2]);
if (towers[2].size() >= N) {
if (min > count) {
min = count;
result = route.toString();
}
return;
}
int length = route.length();
// i번 타워에서 j번 타워로 옮기기
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (i==j) continue;
// 이전 이동과 반대되는 이동(왔다갔다)은 PASS
if (prevPush == i && prevPop == j) continue;
if (towers[i].size() <= 0) continue;
if (towers[j].size() == 0 || towers[j].peek() > towers[i].peek()) {
moveDisk(i, j); // 옮기기
route.append(i).append(' ').append(j).append('\n');
dfs(count + 1, i, j, route); // 재귀함수 호출
moveDisk(j, i); // 원상복구
route.delete(length, route.length()-1);
}
}
}
}
private static void moveDisk(int popTower, int pushTower) {
int popDisk = towers[popTower].pop();
towers[pushTower].push(popDisk);
}
}
public class Main {
static int N, moveCount;
static Stack<Integer>[] towers;
static StringBuilder result;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
moveCount = 0;
result = new StringBuilder();
moveDisks(N, 1, 3, 2);
System.out.println(moveCount);
System.out.println(result);
}
private static void moveDisks(int diskCount, int start, int end, int sub) {
if (diskCount == 1) {
moveCount += 1;
result.append(start).append(' ').append(end).append('\n');
return;
}
// 보조기둥으로 diskCount-1개만큼 옮기기
moveDisks(diskCount - 1, start, sub, end);
// 남은 1개 원판을 목표기둥으로 옮기기
moveCount += 1;
result.append(start).append(' ').append(end).append('\n');
// 보조기둥의 원판들을 목표기둥으로 옮기기
moveDisks(diskCount - 1, sub, end, start);
}
}
문제를 작은 문제로 쪼개야 했다.
문제 해결을 위한 로직은 아래와 같다.
1. N-1개의 원판을 보조기둥으로 옮긴다.
2. 남은 1개의 원판을 목표 기둥으로 옮긴다.
3. 보조기둥에 있는 N-1개의 원판을 목표 기둥으로 옮긴다.
로직을 재귀함수 호출 방식으로 N이 1이 될 때까지 잘게 쪼개 문제를 해결한다.
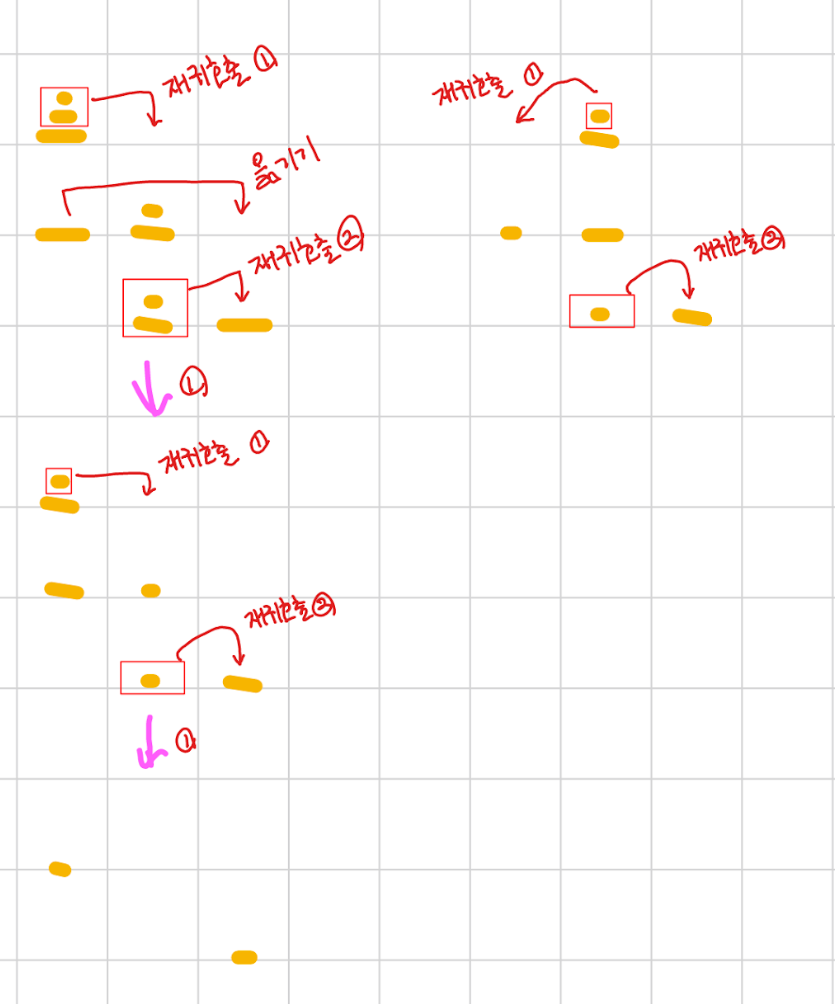
나름 충격적인 풀이법이었다.
이 문제의 해결 방식을 보고
문제를 작은 단위로 쪼개 문제를 해결하는 분할 정복의 느낌을 많이 받았는데,
문제를 가능한 간단한 해결 방법을 생각하는 것, 작은 단위로 쪼개 생각하는 능력을 기르는 훈련이 필요함을 느꼈다.
내가 보려고 만드는 Filler 모음
요세푸스 문제는 다음과 같다.
1번부터 N번까지 N명의 사람이 원을 이루면서 앉아있고, 양의 정수 K(≤ N)가 주어진다.
이제 순서대로 K번째 사람을 제거한다. 한 사람이 제거되면 남은 사람들로 이루어진 원을 따라 이 과정을 계속해 나간다.
이 과정은 N명의 사람이 모두 제거될 때까지 계속된다.
원에서 사람들이 제거되는 순서를 (N, K)-요세푸스 순열이라고 한다.
예를 들어 (7, 3)-요세푸스 순열은 <3, 6, 2, 7, 5, 1, 4>이다.
N과 K가 주어지면 (N, K)-요세푸스 순열을 구하는 프로그램을 작성하시오.
첫째 줄에 N과 K가 빈 칸을 사이에 두고 순서대로 주어진다. (1 ≤ K ≤ N ≤ 5,000)
예제와 같이 요세푸스 순열을 출력한다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;
import java.util.StringTokenizer;
public class Main {
static int N, K, size;
static boolean[] survived;
static int[] ans;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 입력값 입력
N = Integer.parseInt(st.nextToken()); // 사람 수
K = Integer.parseInt(st.nextToken()); // 제거 규칙
survived = new boolean[N + 1]; // 생존 여부를 기록
Arrays.fill(survived, true); // 시작은 모두 생존으로 처리
ans = new int[N]; // 제거된 사람 기록
size = 0; // ans배열의 크기 기록
eliminate();
print();
}
private static void print() {
StringBuilder sb = new StringBuilder();
sb.append('<');
for (int i = 0; i < N; i++) {
if (i < N - 1)
sb.append(ans[i]).append(',').append(' ');
else
sb.append(ans[i]).append('>');
}
System.out.println(sb);
}
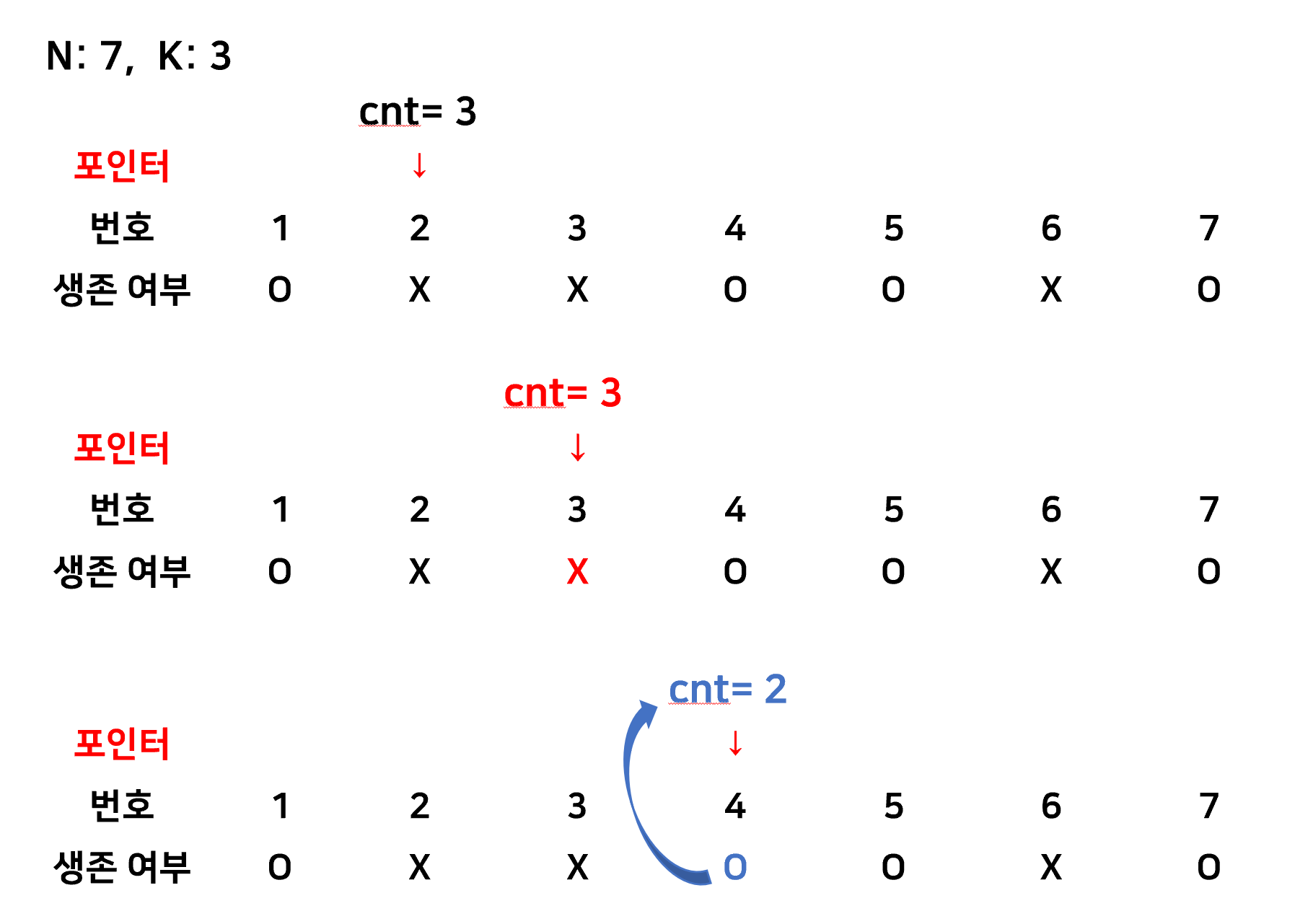
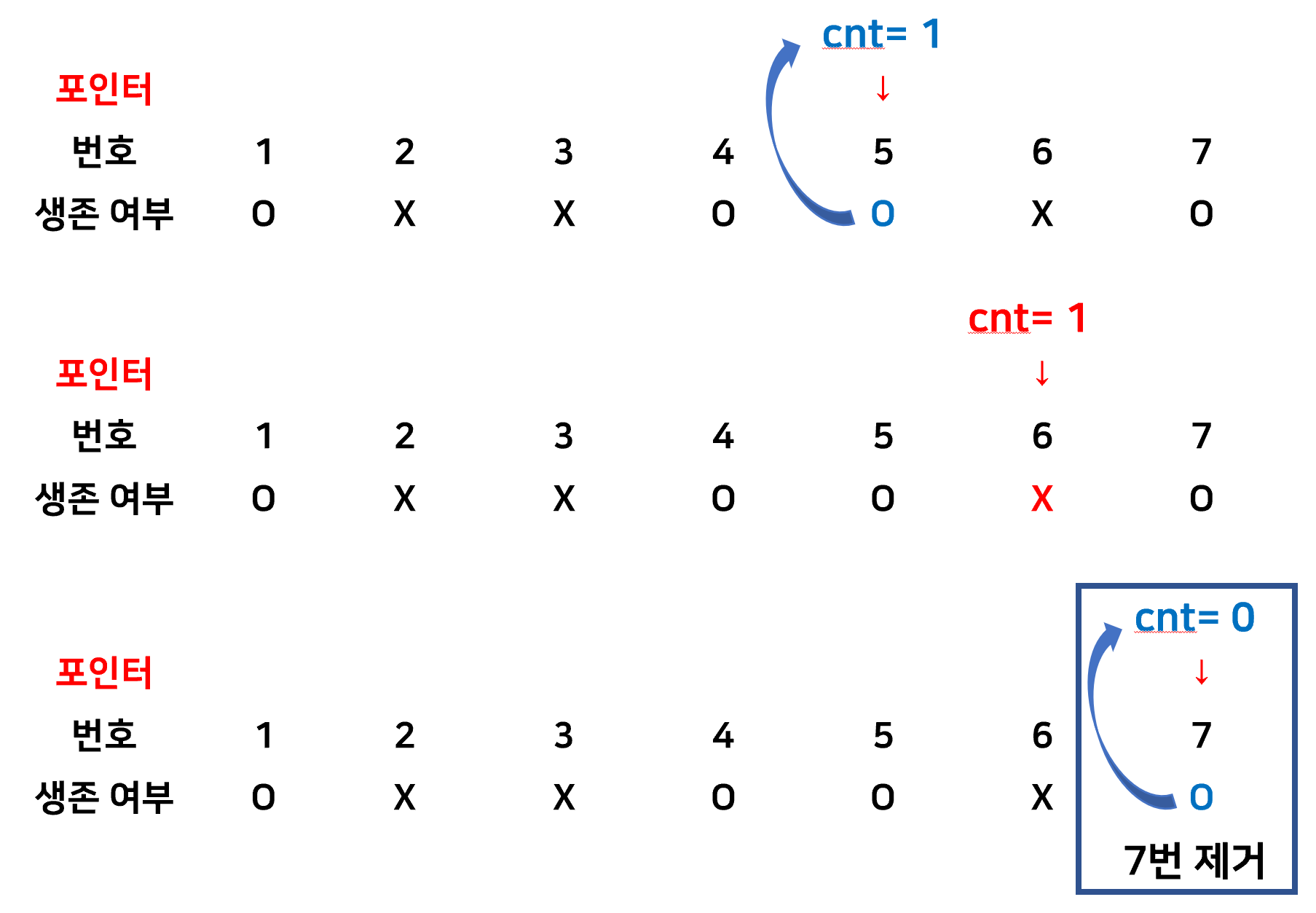
private static void eliminate() {
// 첫번째 제거 대상 제거 후 반복작업 수행
int pointer = K;
survived[K] = false;
ans[size++] = K;
// 모두 제거될 때까지 작업 반복
while (size < N) {
int cnt = K; // 포인터 이동횟수 카운터
while (cnt > 0) {
pointer += 1;
if (pointer>N) pointer %= N; // 모듈러 연산
if (survived[pointer]) cnt -= 1; // 포인터가 생존했을 경우에만 카운트 줄임
}
survived[pointer] = false;
ans[size++] = pointer;
}
}
}
1. survived 배열을 이용해 원에서 제거되었는지 여부를 확인
2. ans 배열에 제거된 사람의 번호를 순서대로 저장
3. 이중 while문을 이용해 pointer를 1개씩 움직여가며 조정했다.
1개씩 움직인 이유는 이미 제거된 사람의 번호는 옮긴 횟수에 들어가지 않아야 하기 때문.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;
import java.util.StringTokenizer;
public class Main {
static int N, K, size;
static boolean[] survived;
static int[] ans;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 입력값 입력
N = Integer.parseInt(st.nextToken()); // 사람 수
K = Integer.parseInt(st.nextToken()); // 제거 규칙
ans = new int[N]; // 제거된 사람 기록
size = 0; // ans배열의 크기 기록
eliminate();
print();
}
private static void print() {
StringBuilder sb = new StringBuilder();
sb.append('<');
for (int i = 0; i < N; i++) {
if (i < N - 1)
sb.append(ans[i]).append(',').append(' ');
else
sb.append(ans[i]).append('>');
}
System.out.println(sb);
}
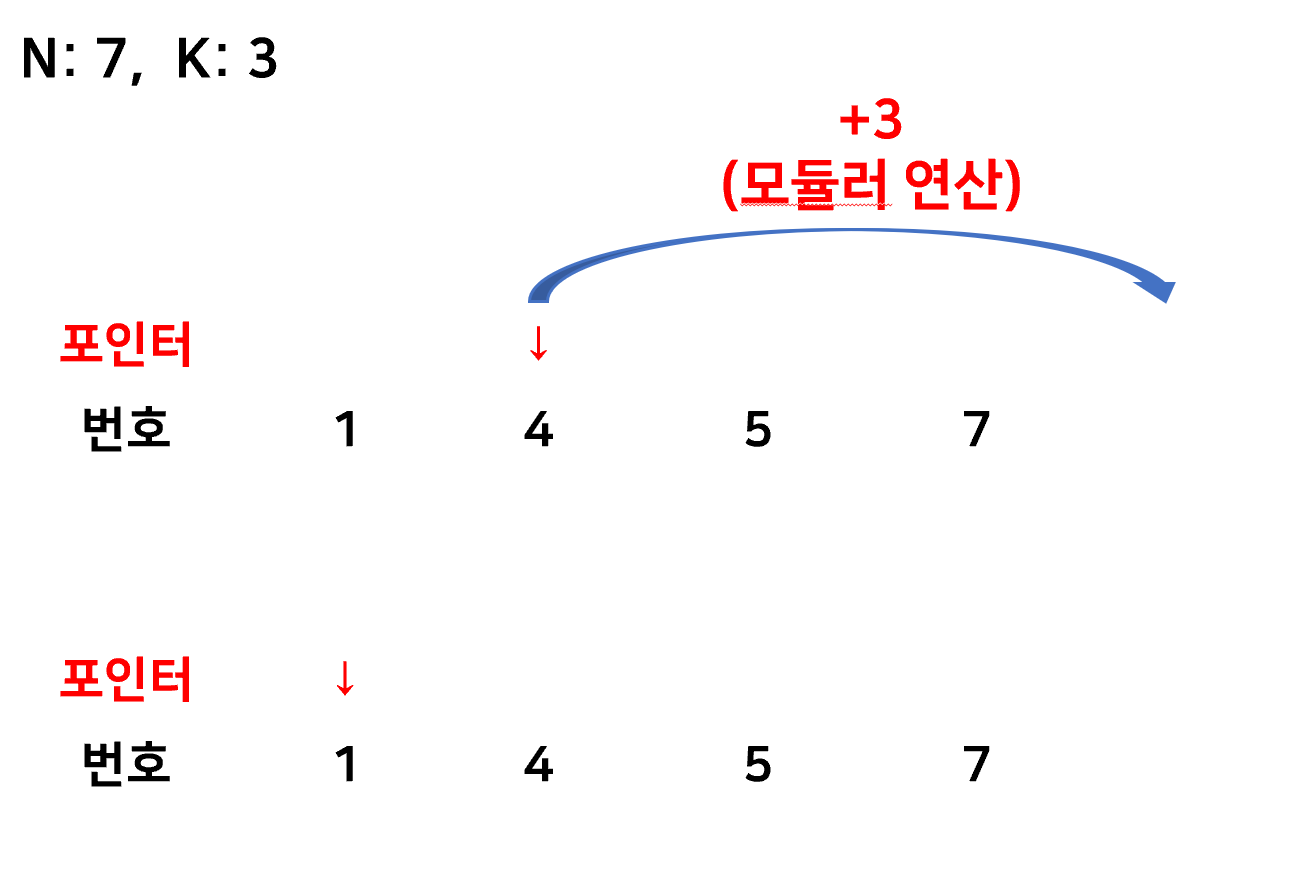
private static void eliminate() {
int pointer = 0;
List<Integer> list = new ArrayList<>();
for (int i = 1; i <= N; i++) {
list.add(i);
}
while (size<N) {
pointer = (pointer + K - 1) % list.size();
ans[size++] = list.remove(pointer);
}
}
}
주요 개선 사항
1. survived 배열 사용하지 않음.
2. 배열 대신 리스트를 생성하여 사람 제거 시 자동으로 인덱스가 당겨지도록 함.
3. pointer를 K만큼 더해 한번에 움직임
이것이 가능한 이유는 리스트 자료구조를 사용해 알아서 제거된 사람을 걸러주는 역할을 했기 때문!
리스트를 사용해도 메모리 사용량에 큰 차이가 없었으며, 실행속도도 5배 가량 빨라졌다.
무조건 배열이 실행속도가 빠른 것은 아님을 알게 되었다.
오히려 리스트 자료구조를 사용하여 K만큼 한번에 건너뛸 수 있어 연산량을 많이 줄일 수 있었다.
중간 요소를 제거하거나 새로 삽입할 경우에는 뒤의 요소들을 한번에 당겨주는 리스트 자료구조가 유리함!
StringBuilder sb = new StringBuilder();
for (int i=0; i<1000000000; i++) {
sb = new StringBuilder();
}
10억회 반복 시 속도 -> 64ms
2. delete() 메서드 사용
StringBuilder sb = new StringBuilder();
for (int i=0; i<1000000000; i++) {
sb.delete(0, sb.length());
}
10억회 반복 시 속도 -> 4ms
3. setLengt() 메서드 사용
StringBuilder sb = new StringBuilder();
for (int i=0; i<1000000000; i++) {
sb = new StringBuilder();
}
10억회 반복 시 속도 -> 4ms
매번 new를 이용해 객체를 새로 생성해 초기화하는 방법은 실행속도 측면에서 가장 최악이었다.
나머지 방법과 비교해 무려 16배 가량 느린 속도를 보여줬다.
그리고 setLength, delete 메서드를 사용해 초기화 하는 방법은 4ms로 비슷한 모습을 보였다.
앞으로 StringBuilder를 초기화해야 할 경우엔 객체 생성은 최대한 피해야 하겠다.
나의 경우에는 delete보단 setLength 메서드가 더 사용하기 간편하기에 setLength를 사용할 것 같다.
그렇다면 실제 문제에 적용하면 어떨까?
조합(Combination) 알고리즘을 사용해 수열에서 필요한 개수만큼 숫자를 뽑은 후,
중복되는 수열을 제거하는 과정에 StringBuilder를 사용했다.
(물론 효율적인 방법이 아니기에 개선 필요.)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
/*
* 비내림차순이어야 하므로, 배열 입력받은 후 정렬하고 조합 작업 시작해야 함.
* 배열을 오름차순으로 정렬하고, 0번 인덱스부터 선택할지 안할지 탐색.
* 최종 수열 완성 시 이미 존재하는지 여부 확인.
*
* 시간복잡도 개선을 위해 배열로 관리.
*/
public class Main {
static int N, M;
static int[] arr;
static int[] tmp;
static String[] pick;
static int size;
static StringBuilder sb;
static StringBuilder ans;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
sb = new StringBuilder();
ans = new StringBuilder();
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
arr = new int[N]; // 원본 배열
tmp = new int[M]; // 숫자 조합 배열
pick = new String[6435]; // 최종 출력할 조합 (최대크기인 8C4 = 70)
size = 0; // 최종 출력할 조합 배열의 크기
// 배열 입력
st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(arr); // 배열 오름차순 정렬
combination(0, 0); // 조합 시작
System.out.println(ans);
}
private static void combination(int aidx, int tidx) {
// 기저조건: tidx가 M에 도달했을 때
if (tidx == M) {
for (int n : tmp) {
sb.append(n).append(' '); // 공백을 추가해서 숫자를 구분
}
// 중복 여부 확인
for (int i = 0; i < size; i++) {
if (pick[i].equals(sb.toString())) {
sb.setLength(0);
return;
}
}
// 중복 없다면 arr배열에 추가 후 정답 출력
pick[size++] = sb.toString();
ans.append(sb).append('\n');
sb.setLength(0);
return;
}
// 불완전 선택 (무시): aidx가 N 이상이면 더 이상 선택할 수 없음
if (aidx >= N) {
return;
}
// 재귀 호출부
for (int i = aidx; i < N; i++) {
tmp[tidx] = arr[i]; // tidx는 M을 넘지 않음
combination(i, tidx + 1); // i를 그대로 넘기므로 중복 조합 허용
}
}
}
여기에서 StringBuilder를 초기화하는 부분만 3가지 방법 각각으로 수정해 비교해보겠다.
???????????????????
setLength가 가장 짧지만 유의미한 차이는 아니였다...
그러니 참고만 하자.
10,000 이하의 자연수로 이루어진 길이 N짜리 수열이 주어진다. 이 수열에서 연속된 수들의 부분합 중에 그 합이 S 이상이
되는 것 중, 가장 짧은 것의 길이를 구하는 프로그램을 작성하시오.
첫째 줄에 N (10 ≤ N < 100,000)과 S (0 < S ≤ 100,000,000)가 주어진다. 둘째 줄에는 수열이 주어진다. 수열의 각 원소는
공백으로 구분되어져 있으며, 10,000이하의 자연수이다.
첫째 줄에 구하고자 하는 최소의 길이를 출력한다.
만일 그러한 합을 만드는 것이 불가능하다면 0을 출력하면 된다.
수열을 입력받으면서, 누적합을 저장하는 배열을 추가로 만들어 누적합을 저장했다.
모든 배열의 합을 일일이 구하지 않아도 누적합에서 빼기 한번으로 부분합을 구할 수 있도록 하기 위함이었다.
(예)
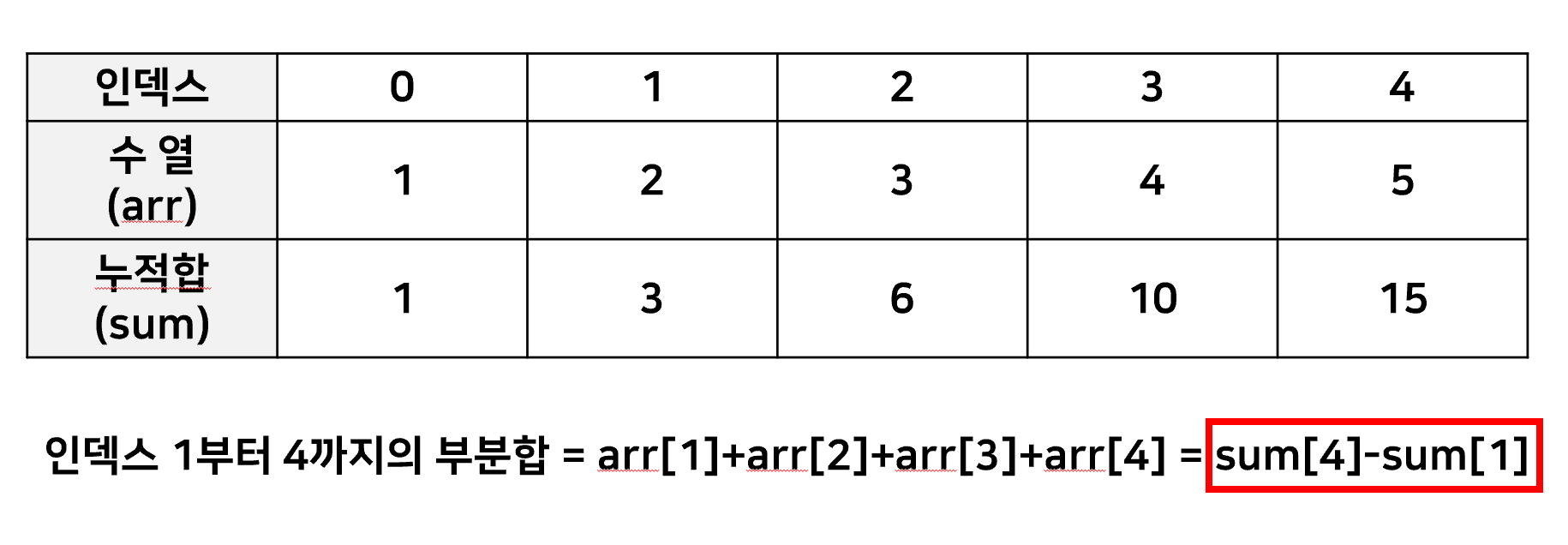
하지만, 이 또한 N개의 인덱스 중 2개를 뽑아 조합하는 경우의 수만큼 작업이 수행되므로,
100000 C 2 = 약 50억 가량의 작업이 소요될 수 있어 시간이 초과하였다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int S = Integer.parseInt(st.nextToken());
int[] arr = new int[N+1];
int[] sum = new int[N+1];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
sum[i] = sum[i - 1] + arr[i];
}
if (S <= 0) {
System.out.println(0);
return;
}
// 부분합 수열의 개수
for (int n=1; n<=N; n++) {
for (int start=1; start<=N-n; start++) {
if (sum[start+n]-sum[start] >= S) {
System.out.println(n);
return;
}
}
}
System.out.println(0);
}
}
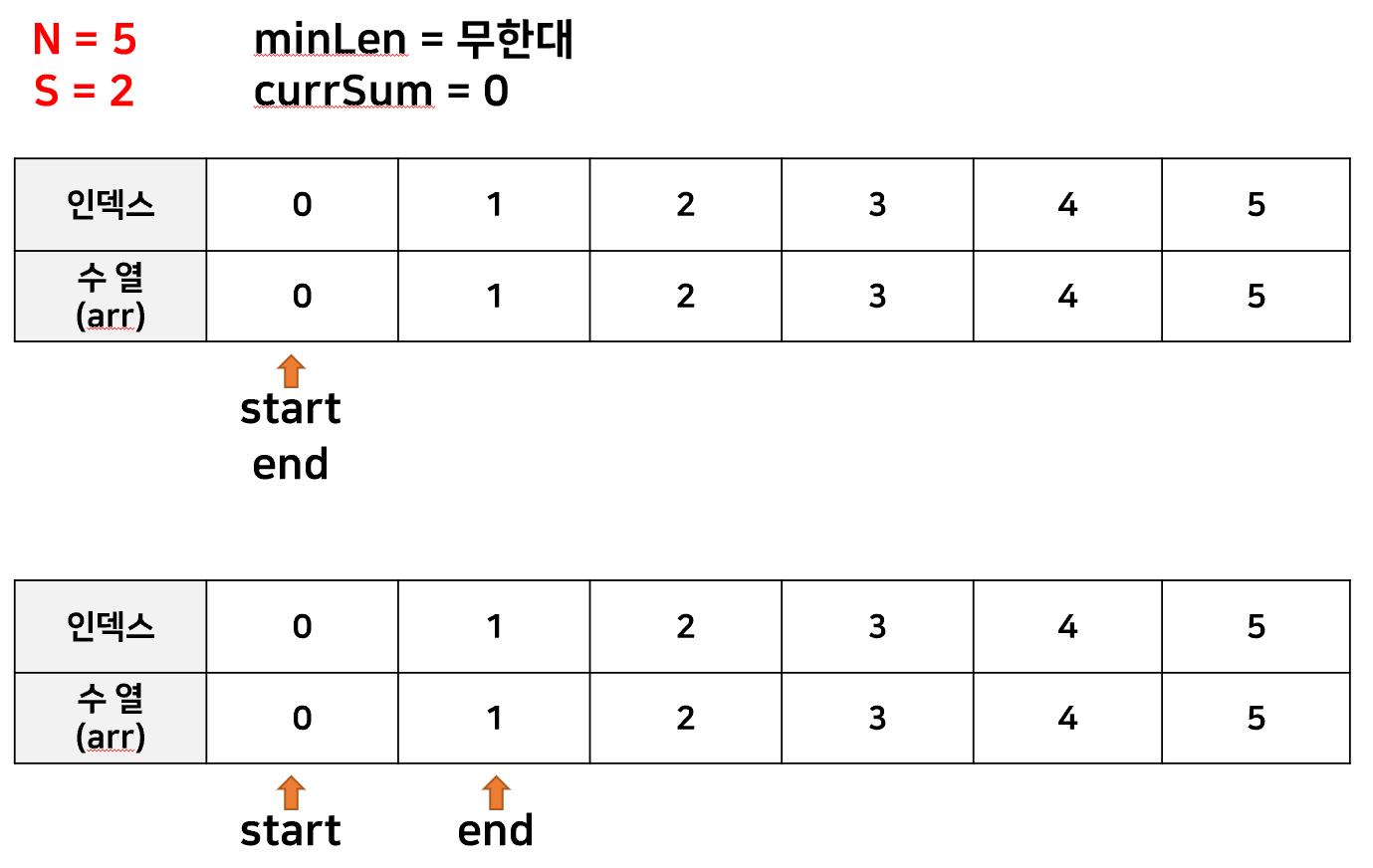
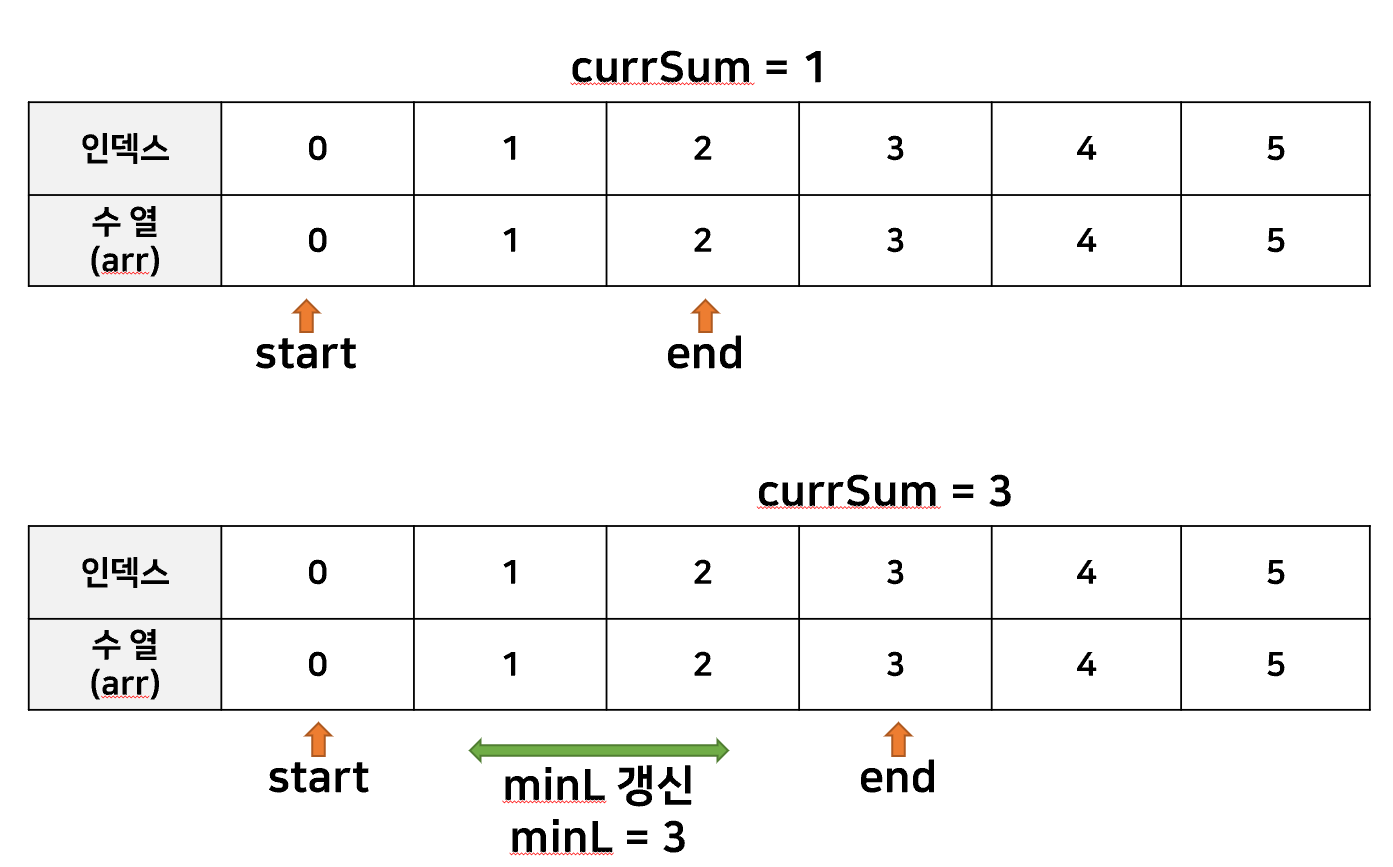
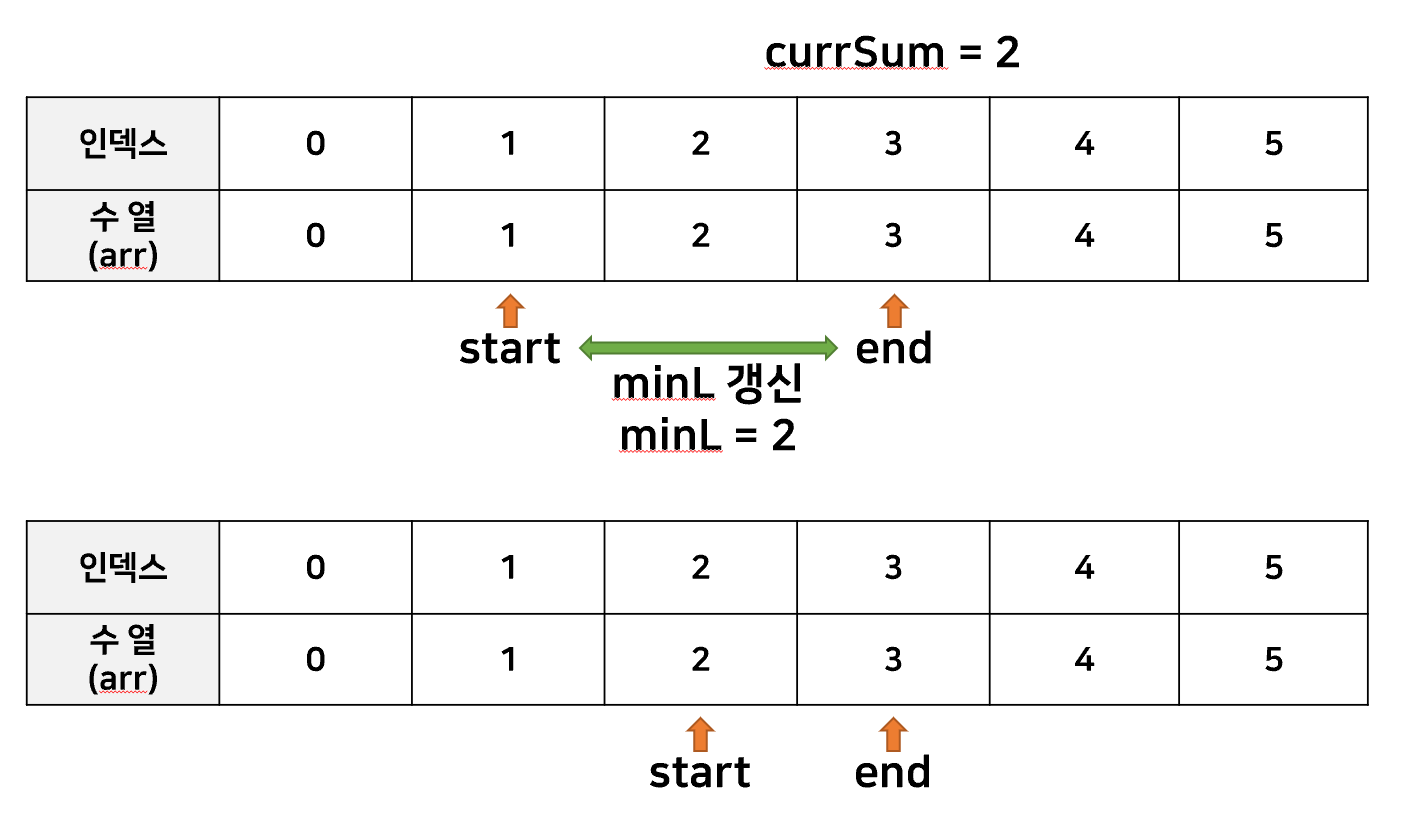
2. 성공
start 포인터와 end 포인터를 각각 선언하여
두 포인터의 위치를 조금씩 조정해가며 최소 개수의 수열을 구하는 방법이 있었다.
이 방법을 사용하면, end포인터와 start포인터 각각 움직이더라도 배열을 1번만 순회하므로
O(n)의 시간복잡도를 가진다고 할 수 있다.
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int S = Integer.parseInt(st.nextToken());
int[] arr = new int[N+2];
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int start = 0;
int end = 0;
int minL = Integer.MAX_VALUE;
int currSum = 0;
while(end <= N+1 && start <= N) {
if (currSum < S) {
currSum += arr[end++];
}
else {
minL = Math.min(minL, end-start);
currSum -= arr[start++];
}
}
if (minL == Integer.MAX_VALUE) {
System.out.println(0);
} else {
System.out.println(minL);
}
}
}
어느덧 싸피 12기 1학기가 지나가고 잡페어 기간이 되었다.
그동안 바쁘다는 핑계로 계속 미루던 SSAFY 12기 비전공자 합격 후기를 적어보고자 한다!!
Samsung Software Academy For Youth 약자다.
삼성과 고용노동부가 크로스! 해서 개발 교육도 시켜주고,
취업박람회, 취업교육 등 취업도 지원해준다
거기다 지원금까지 ...
외쳐 God싸피!
나이
20대 후반
경력
공무원으로 2년 반정도 근무했었다.
전공 (비전공자)
컴공 혹은 프로그래밍과 관련 없는 공대생이다!
관련 공부 경험
프로젝트 경험
전혀 없음
나는 내가 더 흥미를 느끼고 좋아하는 일을 하고 싶었다.
그런 고민을 하던 중 개발이라는 분야를 알게 되었고, Java로 1개월 정도 맛본 후
개발자가 되어 일하겠다는 마음을 먹었다.
비전공자가 개발자로 일하기 위해서는 보통 부트캠프, 국비지원교육을 듣게 되는데,
컴공을 졸업한 지인이 SSAFY를 통해 졸업 후 취업까지 했다는 얘기와 함께
비전공자에겐 SSAFY만한 게 없을 거라는 얘기를 나에게 해주었다.
그렇게 SSAFY의 존재를 알게 되었다.
찾아보니 나에게 아래의 특징들이 나에게 특히 장점으로 느껴졌다.
원서접수를 제외하면 크게 2개로 나누어진다.
1. SW적성진단 + 에세이
2. 인터뷰 (면접)
나는 자격증이나 시험을 보기 전에 항상 공부 전략을 먼저 세운다.
전략을 세우기 위해 정보를 수집해야 하는데,
정보는 보통 이미 합격한 선배들의 합격 수기를 보고 공통되는 부분,
내가 실행할 수 있는 부분 등을 골라낸다.
1. SW적성진단 + 에세이
(1) SW 적성진단
우선 SW 적성진단은
GSAT에서 볼 수 있는 수/추리 논리력 진단 파트와 CT(Computational Thinking) 파트로 나누어 출제되기 때문에
두 가지 모두 공부해야 한다. CT는 쉽게 나오기 때문에 따로 준비하지 않고도 잘 풀었다는 후기를 많이 봤는데,
난 둘다 어려워서 공부가 필요했다.
나는 다니던 직장을 그만두고 도전하는 만큼, 반드시 SSAFY에 붙겠다는 마음이 강력했다.
적성검사 관련 공부를 했던 경험이 전혀 없었고,
정보를 수집하면서 SW적성진단이 에세이보다 좀 더 중요하겠다는 생각(개인적인 추측일 뿐입니다!)에
추려진 책 3권을 모두 풀었다..! (무려 각 3회독 이상)



맨 처음엔 에듀윌 SSAFY를 사서 풀었는데, 책이 해당 시험에 딱 맞춰 만들어져서 좋았다.
그런데 책을 5회독까지 하다 보니 풀이가 외워져서 문제 앞 부분만 봐도 답과 풀이가 생각났다.
더 이상 푸는 의미가 없다고 판단해 GSAT를 추가 구매해 3회독 했다.
GSAT만 보다 보니 수/추리는 대비가 되는데 CT 대비가 부족하다고 판단되어
해커스의 SSAFY 책을 추가 구매해 또 여러번 풀었다.
문제를 풀 땐 스탑워치로 수/추리는 1분 안에, CT는 세트당 8분 이내 다 풀지 못하면 틀린 것으로 간주했고,
틀리거나 확실하게 알지 못하는 것을 체크해 다음 회독 때 그것만 다시 보았다.
이렇게 보니 나 정말 많이 하긴 했네..??
결과적으로 책으로 시험을 준비한 것은 잘 했다고 생각이 든다.
그래서 책을 고민하는 사람들을 위해 대략 추천해보자면,
SSAFY 책 먼저 여러번 풀어보고 유형별 풀이를 모두 익힌 다음,
시간이 남거나 공부가 부족하다는 생각이 들면 GSAT 책을 추가로 보는 것을 추천하겠다!
또 스탑워치로 시간을 재서 수/추리는 1분 이내 , CT는 1세트당 7분30초 이내 빠르게 푸는 연습을 반드시 하세요!
(2) 에세이
자소서를 쓴 경험이 전무했기에, 쓰면서 스트레스를 많이 받았다.
가장 중요하다고 생각하는 것은
"자기 자신에 대해 진지하게 알아가는 시간을 다시 한번 가져보는 것" 이다.
그래야 면접 때도 문제가 없다.
직장을 그만두면서 나에 대해 다시 생각하는 시간을 많이 가졌는데도
다시 정리하려니 힘들었다.
결과적으로 에세이에 내가 녹여낸 내용은 대략 아래와 같다.
- 왜 개발자가 되고 싶은지 (동기)
- 개발자가 되기 위해 어떤 노력, 공부를 했는지 + 노력했지만 부족하다고 느낀 점 (구체적으로)
👉 그래서 SSAFY에서 부족한 점을 채우고자 지원했습니다~ 로 연결
- 많은 교육 중 왜 하필 SSAFY 여야만 하는지
- SSAFY에 들어간다면 어떻게 공부할지 or 어떤 프로젝트를 하고 싶은지
👉 과거 공부 열심히 해서 성과 낸 것을 함께 어필했음
PT면접 + 인성면접으로 구성.
면접 스터디를 통해 준비했다.
스터디를 할까 말까 고민을 많이 했는데( I 특),
해보니 직접 말하는 연습이 확실히 도움 됐다.
내성적인 사람일수록 더더욱 큰 용기를 내 스터디에 참가해보는게 좋을 것 같다.
면접 스터디
장점
1. 사람들 앞에서 말해보는 연습이 된다 (최고의 장점)
2. 면접 준비를 더 열심히 할 수 있는 강제성이 부여된다.
3. 전공자의 시각, 타인의 시각에서 새로운 의견을 들을 수 있다.
4. IT관련 정보 수집 시 나눠서 할 수 있어 더 많은 정보를 접할 수 있다.
단점
1. 오프라인의 경우, 이동 시간이 걸리고, 장소 섭외 비용도 발생한다.
2. 비슷한 수준의 스터디원이 모일 경우, 서로에게 도움이 되지 않을 수 있다.
(1) PT면접
1. 다들 알다시피 강민혁 선생님의 Youtube를 반드시 먼저 보고 구조를 익히기!
https://www.youtube.com/watch?v=DOvCIrwMPbQ
무경험자인 나는 이 영상을 보고 익혀 실전에 활용했다.
스터디를 한다면 아마 누군가 이 영상을 올려줄 것이다. 아무도 올리는 사람이 없다면
여러분이 직접 올리고 이대로 연습하자고 제안해보세요!
기가 막힌 아이디어를 내는 것보다 논리적으로 문제점, 해결방안, 해결방안에서 발생할 수 있는 어려움까지 연결하는 것에 집중할 것.
2. IT 이슈, 지식 습득
면접에서 평소 IT 이슈나 요즘 핫한 기술들에 관심이 많음을 어필하는 것이 중요하다.
PT면접에서도 IT 지식이 있어야 해결책, 아이디어가 나온다.
과학기술정보통신부 블로그, IT 관련 뉴스기사를 찾아보기도 했지만,
나는 책을 빌려 본 것이 더 도움 되었다.
IoT, AIoT, AI, 생성형AI, 로봇, 블록체인, 스마트팩토리, 스마트팜, VR, XR, 메타버스 등등...
핵심 기술들의 특징, 장단점, 문제점, 해결방안을 정리했다.


오픽 IH 이상을 목표로 공부를 시작하려 한다.
자격증 공부는 공부 전략을 잘 짜는 것이 중요하다고 생각하기 때문에
합격한 선배들의 후기들을 살펴보고 공통적으로 나오는 공부 팁, 공부 방법들을 대략 정리했다.
👉 영상만 활용해도 되지만, 강의 수가 많고 정리되지 않은 면이 있기 때문에 정리된 형태인 책을 구매해 효율 높일 수 있음
👉 오픽이 어떤 시험인지, 점수를 잘 받기 위해선 어떻게 해야하는지 등을 파악하며 들을 것
👉 답변 구조를 만들어 둘 것
👉 필러로 사용할 용어들을 많이 준비해 둘 것!!
** 필러 : um, you know, that's a good question 등의 양념같은 구문들
IM 시리즈, IH 시리즈 영상 개수는 모두 52개이고, 영상 1개당 대략 15분 정도이다.
우선 하루에 2~3개 정도씩 보는 것을 목표로 공부할 예정!
👉 영상 보며 짠 구조대로 한국어로 먼저 써보기 (필러를 반드시 넣어서 쓸 것)
👉 영어로 말해보기
👉 GPT, 스픽 활용해서 말하고 교정받기!!
👉 여우오픽 모의고사, 해커스 오픽 활용
👉 강지완 오픽 영상 찾아보기
기본 오픽 응시료는 84,000원이다.
휴대폰 통신사 KT, SKT 중에서 사용하는 경우,
멤버십 혜택으로 응시료 5% 할인 받을 수 있다.
대학교 재학생인 경우, 약 18% 할인이 들어간다.
많은 대학교가 협약되어 있는 것으로 보이니 재학생이라면 반드시 확인할 것
난 졸업생이라 불가 ㅠㅠ
https://apply.jobaba.net/special/GGtestfees/main.do#!
잡아바어플라이 | 통합접수시스템
신청하기 지원 항목을 선택하세요 생년월일 지역
apply.jobaba.net
현재 거주하고 있는 시, 도 별로 특정 자격시험 응시료를 지원하는 사업을 대부분 하고 있다.
다만 현재는 경기도를 포함 대부분의 지자체 예산이 소진되어 나의 경우에는 혜택을 못 받을 것 같다.
내년 봄-여름은 되어야 다시 시작하지 않을까..
수를 처리하는 것은 통계학에서 상당히 중요한 일이다. 통계학에서 N개의 수를 대표하는 기본 통계값에는
다음과 같은 것들이 있다. 단, N은 홀수라고 가정하자.
N개의 수가 주어졌을 때, 네 가지 기본 통계값을 구하는 프로그램을 작성하시오.
첫째 줄에 수의 개수 N(1 ≤ N ≤ 500,000)이 주어진다. 단, N은 홀수이다. 그 다음 N개의 줄에는 정수들이 주어진다.
입력되는 정수의 절댓값은 4,000을 넘지 않는다.
첫째 줄에는 산술평균을 출력한다. 소수점 이하 첫째 자리에서 반올림한 값을 출력한다.
둘째 줄에는 중앙값을 출력한다.
셋째 줄에는 최빈값을 출력한다. 여러 개 있을 때에는 최빈값 중 두 번째로 작은 값을 출력한다.
넷째 줄에는 범위를 출력한다.
1. 수를 입력받아 배열에 저장할 때, 수의 총합인 sum변수를 선언해 총합을 구해두었다.
2. 최빈수를 구하기 위해 카운트 배열을 쓰고자 했으나,
수 범위를 500,000까지인 것으로 잘못 읽어 메모리 초과 발생을 우려해 Map 자료형을 선택했다.
또한 최빈수가 여러개일 때 그 수를 저장하기 위해 리스트를 사용했다.
3. 또한 Arrays.sort를 통해 최대값과 최소값(arr[N-1]-arr[0]) 차이, 중앙값(arr[N/2])을 얻어냈다.
>> 결과적으로 최빈수를 구하는 과정에서 list를 만들고, Collections.sort를 사용한 것, map자료형을 사용한 것이
실행속도를 늦춘 원인으로 판단했다. 크기 8001짜리 카운트 배열을 활용해 구했다면 훨씬 빠를 것으로 예상했다.
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringBuilder sb = new StringBuilder();
Map<Integer, Integer> map = new HashMap<>(); // 최빈값 계산
int n = sc.nextInt();
int[] arr = new int[n];
int sum = 0;
// 입력받으면서 총합 구함
for (int i = 0; i < n; i++) {
int tmp = sc.nextInt();
arr[i] = tmp;
sum += tmp;
// 해당 값의 빈도를 카운트
if (map.containsKey(tmp)) {
map.put(tmp, map.get(tmp) + 1);
} else {
map.put(tmp, 1);
}
}
// 산술평균 출력
sb.append(Math.round((double) sum / n)).append('\n');
// 중앙값 계산
Arrays.sort(arr); // 오름차순 정렬
sb.append(arr[n / 2]).append('\n');
// 최빈값 계산
int max = 0;
List<Integer> list = new ArrayList<>();
for (int key : map.keySet()) {
if (map.get(key) > max) {
max = map.get(key);
list.clear();
list.add(key);
} else if (map.get(key) == max) {
list.add(key);
}
}
Collections.sort(list);
if (list.size() <= 1) {
sb.append(list.get(0)).append('\n');
} else {
sb.append(list.get(1)).append('\n');
}
// 최대값, 최소값 차이
sb.append(arr[n - 1] - arr[0]);
System.out.println(sb);
}
}
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
StringBuilder sb = new StringBuilder();
int n = sc.nextInt();
int[] arr = new int[n];
int[] count = new int[8001]; // -4000 ~ 4000 범위를 담을 수 있는 배열
int sum = 0;
int maxFrequency = 0;
// 입력받으면서 총합과 빈도 계산
for (int i = 0; i < n; i++) {
int value = sc.nextInt();
arr[i] = value;
sum += value;
count[value + 4000]++; // -4000 ~ 4000을 0 ~ 8000으로 매핑
maxFrequency = Math.max(maxFrequency, count[value + 4000]);
}
// 산술평균 계산 (반올림)
sb.append(Math.round((double) sum / n)).append('\n');
// 중앙값 계산을 위해 정렬
Arrays.sort(arr);
sb.append(arr[n / 2]).append('\n');
// 최빈값 계산
int max = Integer.MAX_VALUE;
boolean foundSecond = false;
for (int i = 0; i < count.length; i++) {
if (count[i] == maxFrequency) {
if (max == Integer.MAX_VALUE) {
max = i - 4000;
} else if (!foundSecond) {
max = i - 4000;
foundSecond = true;
}
}
}
sb.append(mode).append('\n');
// 최대값과 최소값의 차이 계산
sb.append(arr[n - 1] - arr[0]).append('\n');
// 결과 출력
System.out.println(sb);
}
}